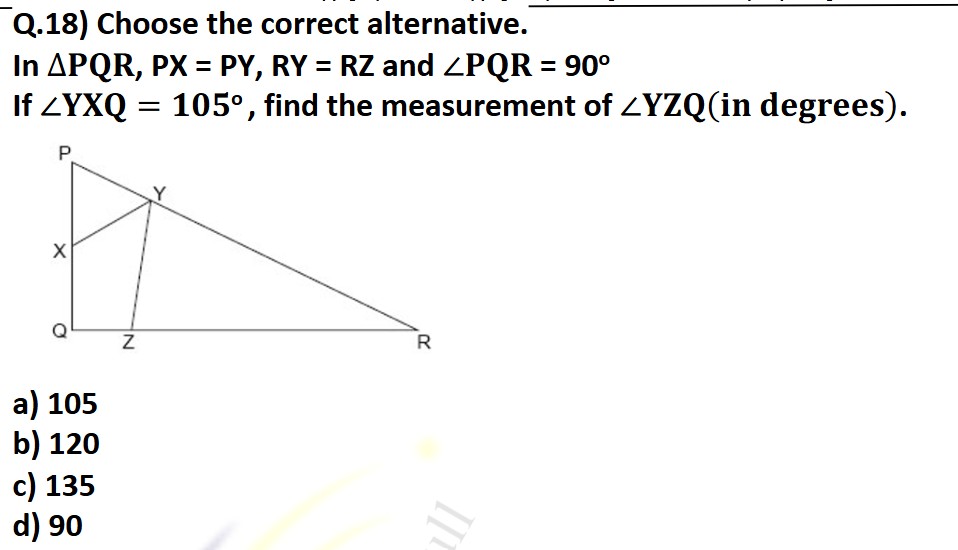
VARC Question, can anyone please explain me how to approch this type of questions and what they mean to say?
Atharva Shelke CATKing Student
Started 4 months ago in CAT, CAT Quantitative Ability, Arithmetic
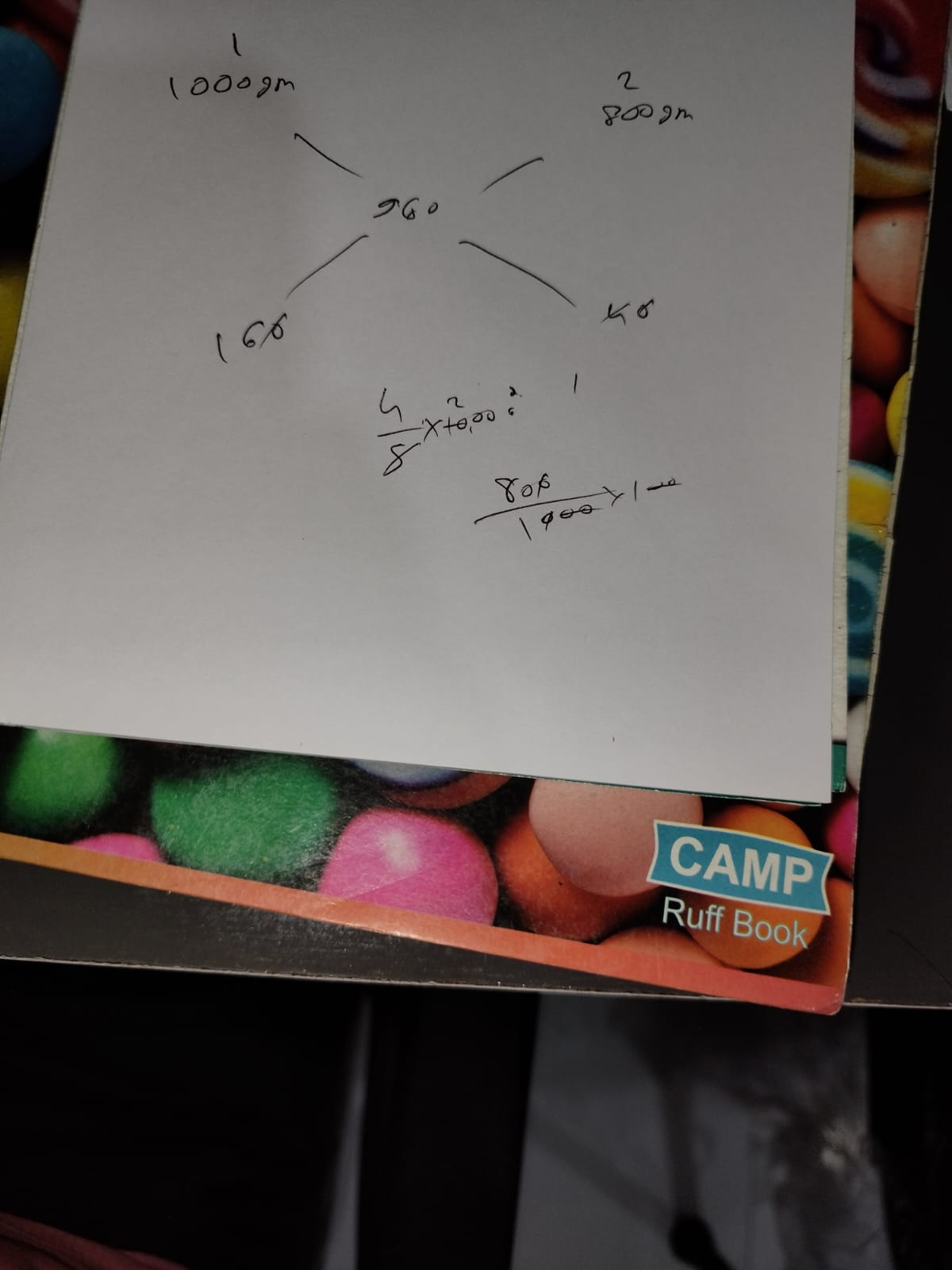
A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is
Is my approach wrong?? can anyone please explain it because i get it right but the actual step was different than mine, please!
Please solve this doubt
VARC doubt
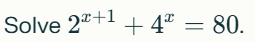
Quant doubt
Please answer this doubt
Club 99%ile DILR
DILR Decoded: How did you choose the right sets?
Club 99%ile QA
Quant at 99: Did you rely on concepts or speed tricks?
Admin CATKing Student
Started 5 months ago in CAT, CAT Verbal Ability, Reading Comprehension
Club 99%le VARC
Cracked 99+%ile in VARC? Drop your golden rules here!
The sum of 2n terms of A.P {1, 5, 9, 13.....} is greater than sum of n terms of A.B = [56, 58, 60...) What is the smallest value n can take? A. 9 | Correct Answer A. 619 | | Explanation | Gc 12 oe ai | Video Solution BD. 14 .