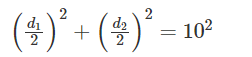CATKing Forum
Home FAQs
Add New Thread
Privacy Policy Articles

Live Updates

• CATKing has launched new chat bot.

• New video on Logs has been released.

13.2K Learners
asked the doubt

CAT 2021 Question Paper Slot 3 | All Questions

Previous Year Questions

    01.

    Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.

    For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.

     

     

    01.

    5 ml of content from bottle A is mixed with 5 ml of content from bottle B. The resultant mixture, when tested, detects the presence of I. If it is known that bottle A contains only P, what BEST can be concluded about the volume of I in bottle B?
    Option A is the correct answer.

    Video Explanation

    Explanatory Answer

    Now 50 ml of content in bottle A is 100% pure of which 5 ml is mixed with 5 ml from bottle B and
    an impurity is detected. Now we can only detect an impurity if there is 10% or more impure
    material.
    Now Bottle A has 100% and we need final mixture to have 90% or less impurity which means that
    Maximum % of P which bottle B can have is 80%.
    This means that impurity content in bottle B is minimum 10ml and can be more than 10 too.
    Thus Option A is the correct answer. 

    02.

    There are four bottles. Each bottle is known to contain only P or only I. They will be considered to be "collectively ready for despatch" if all of them contain only P. In minimum how many tests, is it possible to ascertain whether these four bottles are "collectively ready for despatch"?
    Answer : 1

    Video Explanation

    Explanatory Answer

    Now either a bottle has 100% P or 0% P.
    Let’s assume that 3 are 100% pure and 1 is 0% pure, so now if we mix all 4 together
    Weighted average = (3*100 + 1*0)/4 = 75%
    As per question if the impurity is more than 10% we will be able to detect it, thus only 1 test is
    enough to determine if the bottles are ready for despatch.

    03.

    There are four bottles. It is known that three of these bottles contain only P, while the remaining one contains 80% P and 20% I. What is the minimum number of tests required to definitely identify the bottle containing some amount of I?
    Answer : 2

    Video Explanation

    Explanatory Answer

    We have 3 bottles with 100% P and 1 bottle with 20% impurity
    Let’s select 2 bottles at random and mix them completely, we will end up with 2 cases
    Case 1 – Both bottles test pure, then we take one of these bottles and test it with one of the two
    remaining bottles. It will either come out as pure again or it will show presence of impurity.
    We need 2 tests in this case.
    Case 2 – We find an impurity presence in one of the bottles, again we take one of the 2 bottles
    and test it with 1 of the 2 remaining bottles. It will It will either come out as pure again or it will
    show presence of impurity.
    We need 2 tests in this case too.
    Thus we need a minimum of 2 tests to identify the bottle with the impurity. 

    04.

    There are four bottles. It is known that either one or two of these bottles contain(s) only P, while the remaining ones contain 85% P and 15% I. What is the minimum number of tests required to ascertain the exact number of bottles containing only P?
    Option A is the correct answer.

    Video Explanation

    Explanatory Answer

    Answer- 1
    We will take the weighted average approach here
    Case 1 – 1 Bottle has 100% P and 3 bottles have 85% P
    Weighted average = (1*100 + 3*85)/4 = 88.75%
    Impurity will be detected
    Case 2 - 2 Bottles has 100% P and 2 bottles have 85% P
    Weighted average = (2*100 + 2*85)/4 = 92.5%
    Impurity will not be detected
    We can see that only 1 test will be enough to determine the total number of bottles with 100%
    purity.

    02.

    The figure above shows the schedule of four employees – Abani, Bahni, Danni and Tinni – whom Dhoni supervised in 2020. Altogether there were five projects which started and concluded in 2020 in which they were involved. For each of these projects and for each employee, the starting day was at the beginning of a month and the concluding day was the end of a month, and these are indicated by the left and right end points of the corresponding horizontal bars. The number within each bar indicates the percentage of assigned work completed by the employee for that project, as assessed by Dhoni.

    For each employee, his/her total project-month (in 2020) is the sum of the number of months (s)he worked across the five project, while his/her annual completion index is the weightage average of the completion percentage assigned from the different projects, with the weights being the corresponding number of months (s)he worked in these projects. For each project, the total employee-month is the sum of the number of months four employees worked in this project, while its completion index is the weightage average of the completion percentage assigned for the employees who worked in this project, with the weights being the corresponding number of months they worked in this project.

    01.

    Which of the following statements is/are true?

    I: The total project-month was the same for the four employees.
    II: The total employee-month was the same for the five projects.
    Option D is the correct answer.

    Video Explanation

    Explanatory Answer

    02.

    Which employees did not work in multiple projects for any of the months in 2020?
    Option D is the correct answer.

    Video Explanation

    Explanatory Answer

    03.

    The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
    Option D is the correct answer.

    Video Explanation

    Explanatory Answer

    Project 1 & 2 as well as Project 3 & 4 have the same number of months but in the options we only
    have Project 3 & 4.

    04.

    The list of employees in decreasing order of annual completion index is:
    Option C is the correct answer.

    Video Explanation

    Explanatory Answer

    03.

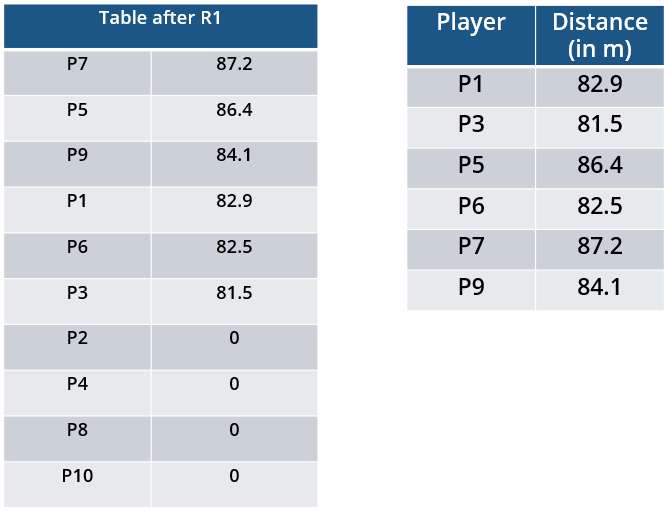
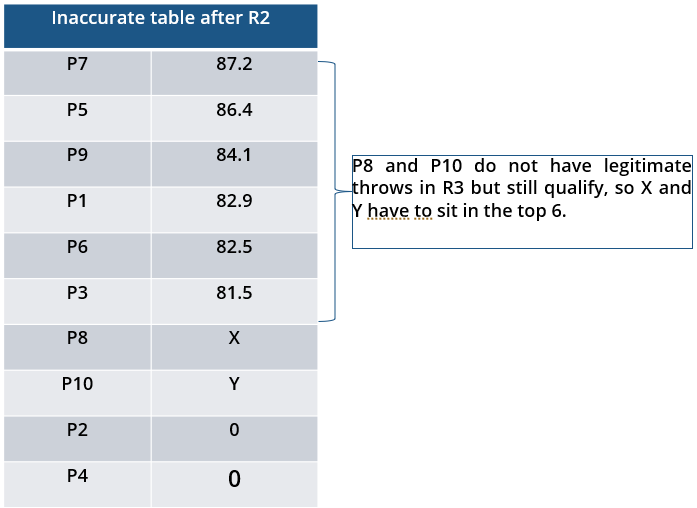
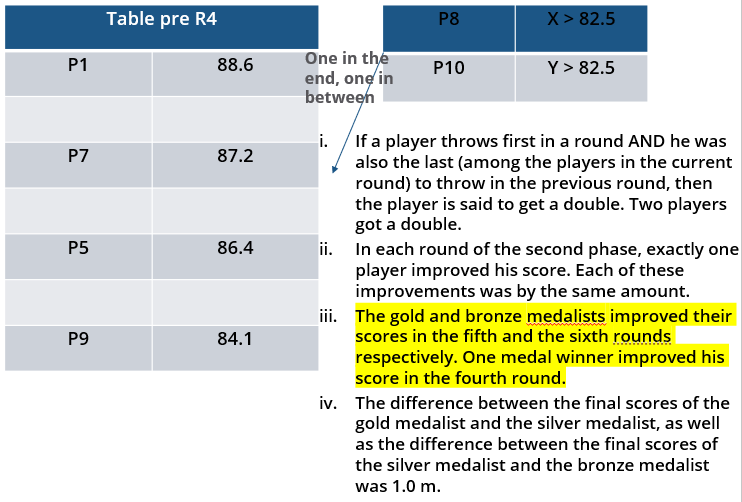
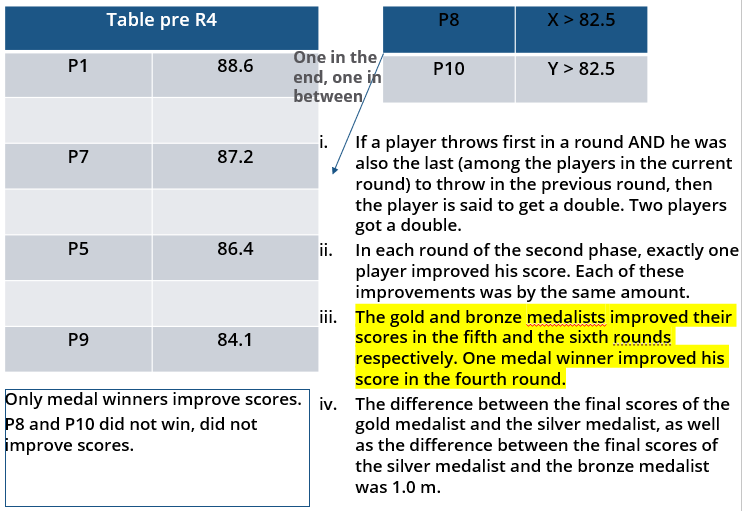
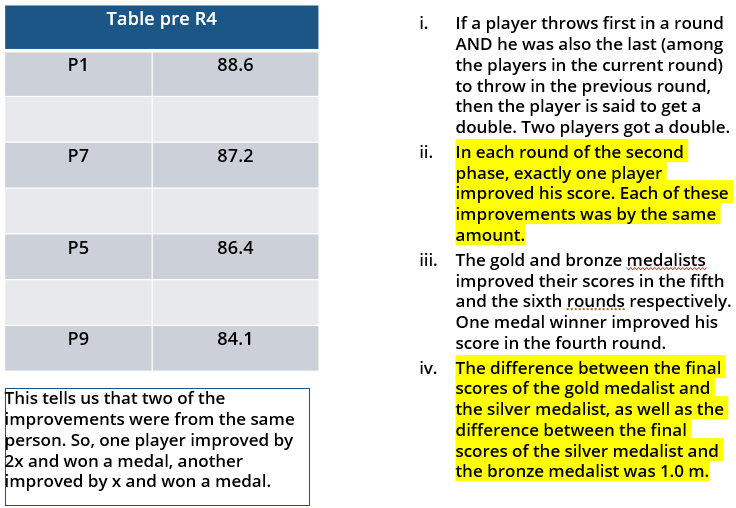
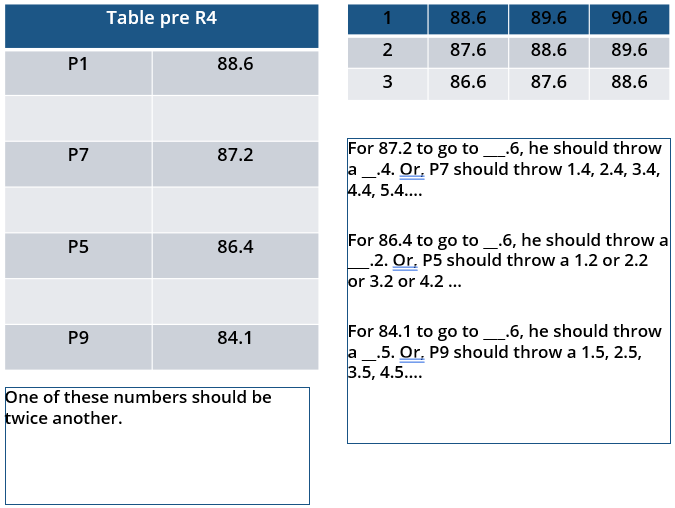
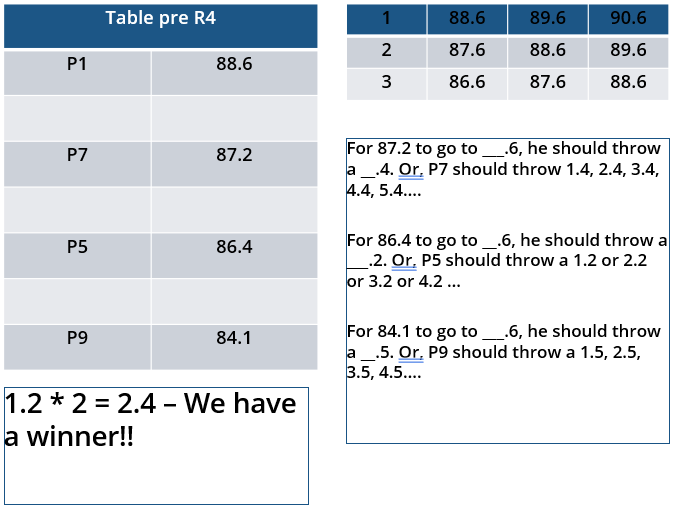
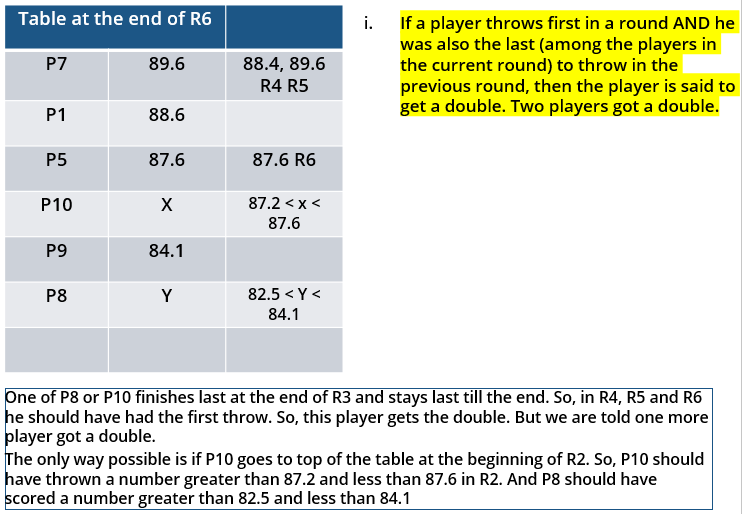
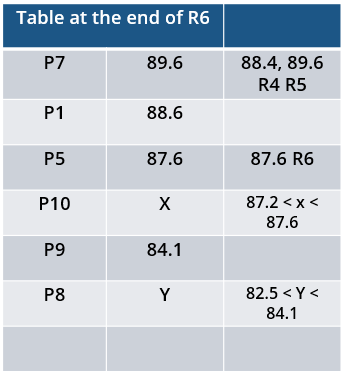
    10 players – P1, P2, … , P10 - competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a 'valid' one. For an invalid throw, the distance is taken as zero. A player's score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round. 

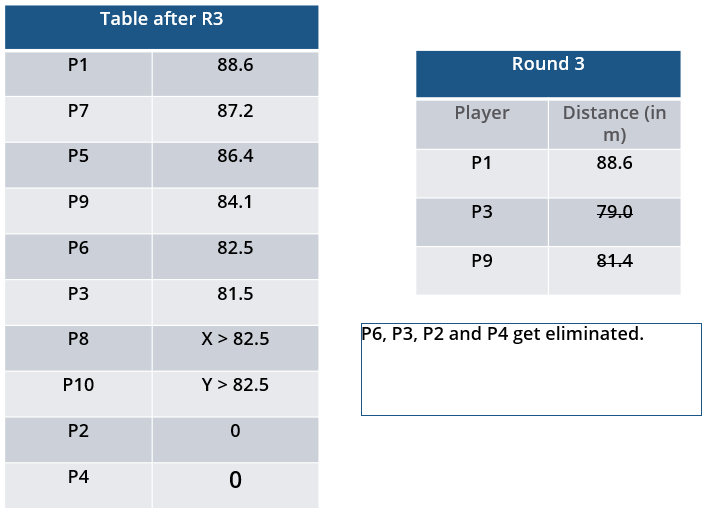
    In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.

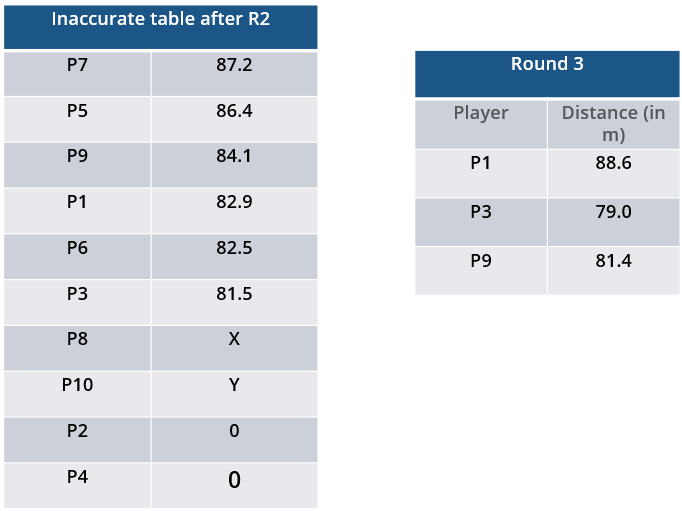
    All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.

    Distances covered by all the valid throws in the first round

    Player Distance (in m)
    P1 82.9
    P3 81.5
    P5 86.4
    P6 82.5
    P7 87.2
    P9 84.1

    Distances covered by all the valid throws in the third round

    Player Distance (in m)
    P1 88.6
    P3 79.0
    P9 81.4

     The following facts are also known.

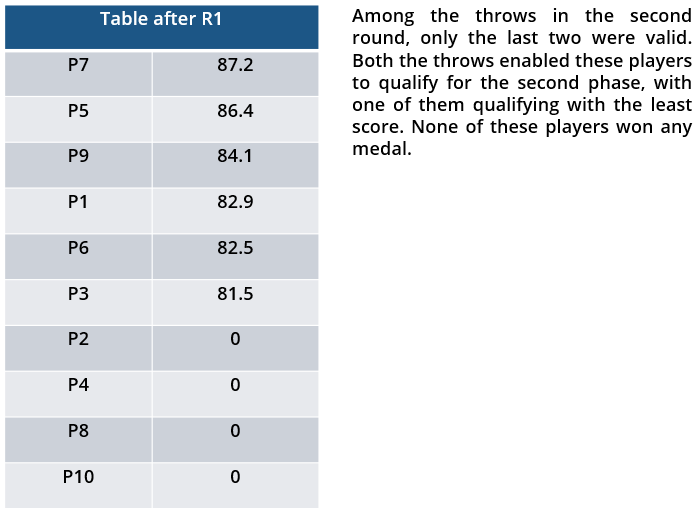
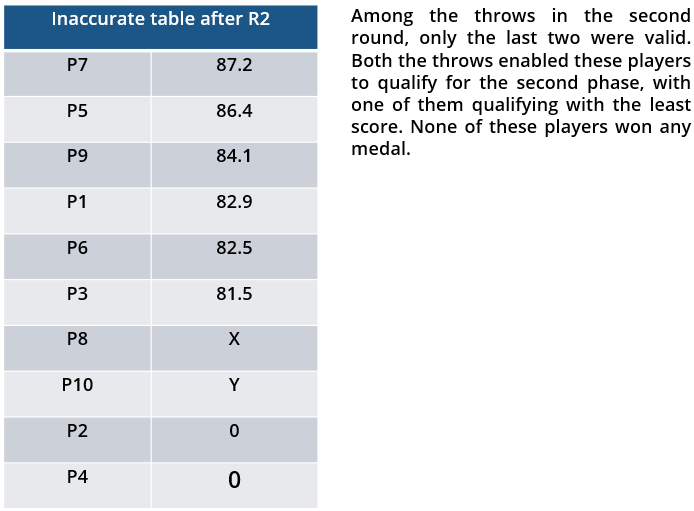
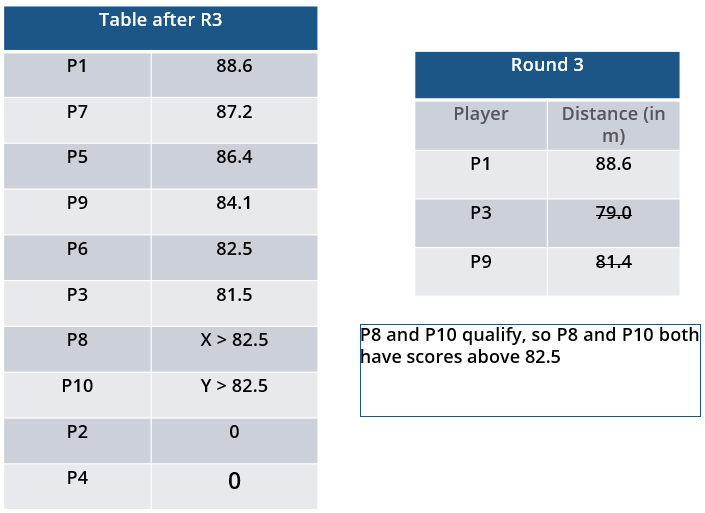
    i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal. 

    ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.

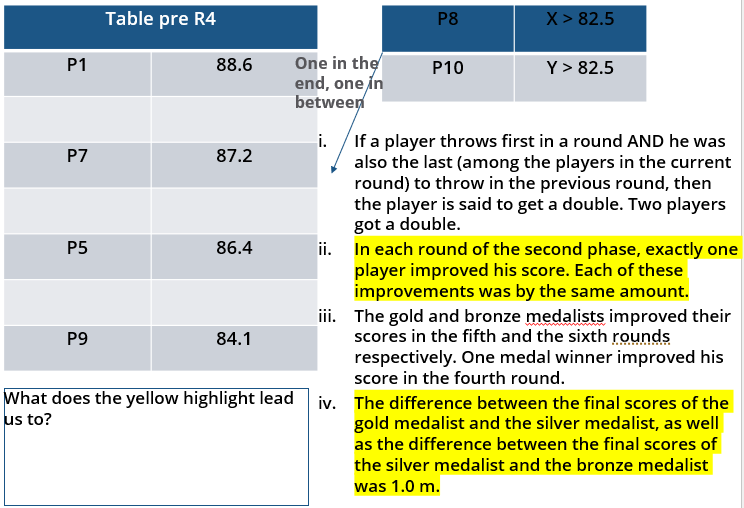
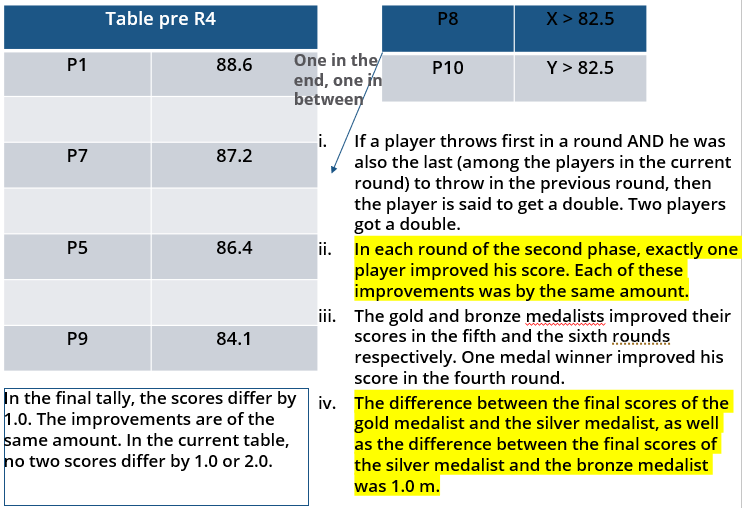
    iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount. 

    iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round. 

    v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.

     

     

    01.

    Which two players got the double?
    Option D is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    02.

    Who won the silver medal?
    Option A is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    03.

    Who threw the last javelin in the event?
    Option B is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    04.

    What was the final score (in m) of the silver-medalist?
    Option D is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    05.

    Which of the following can be the final score (in m) of P8?
    Option B is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    06.

    By how much did the gold medalist improve his score (in m) in the second phase?
    Option C is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    Set 2

    04.

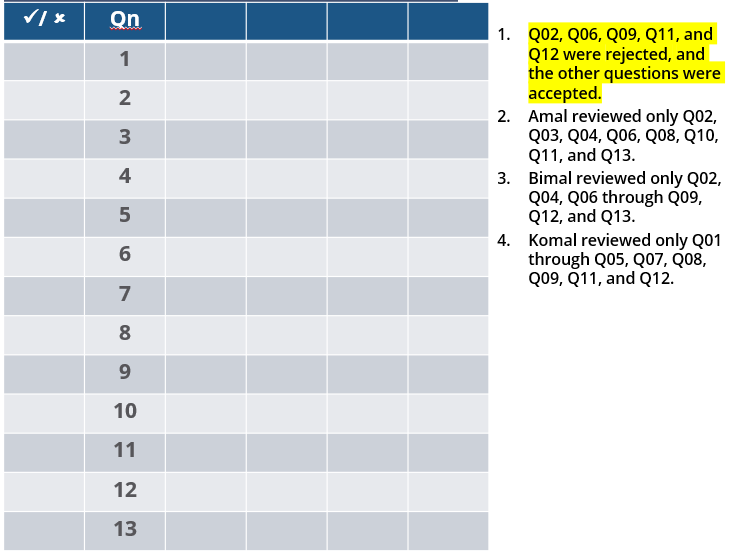
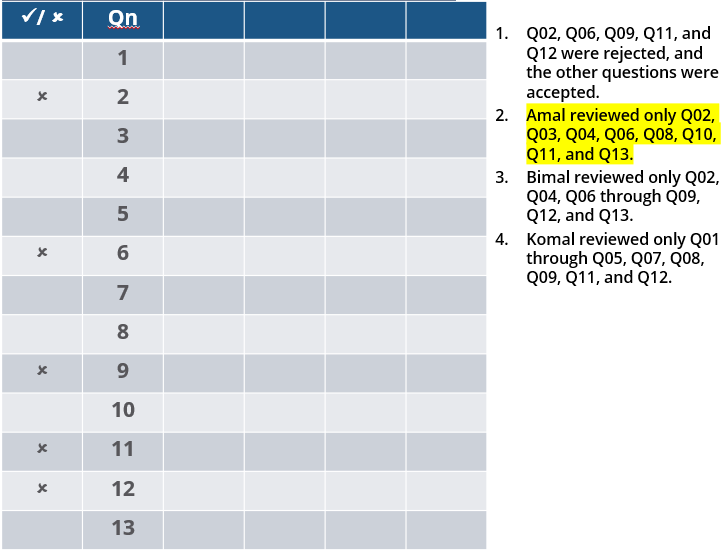
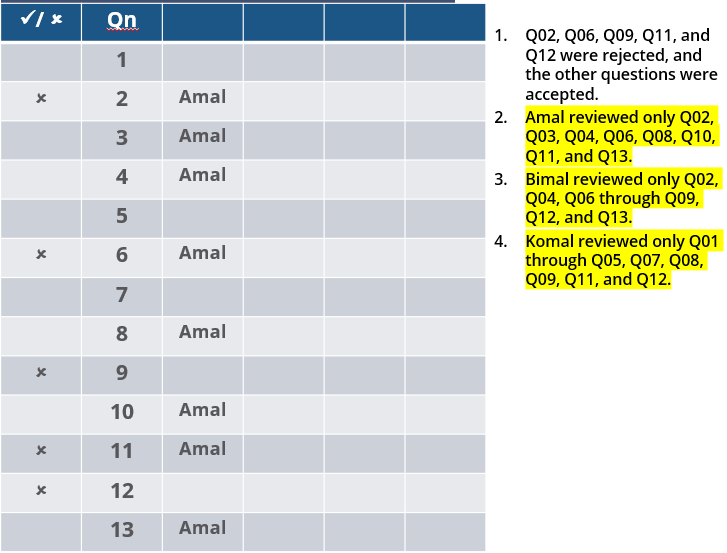
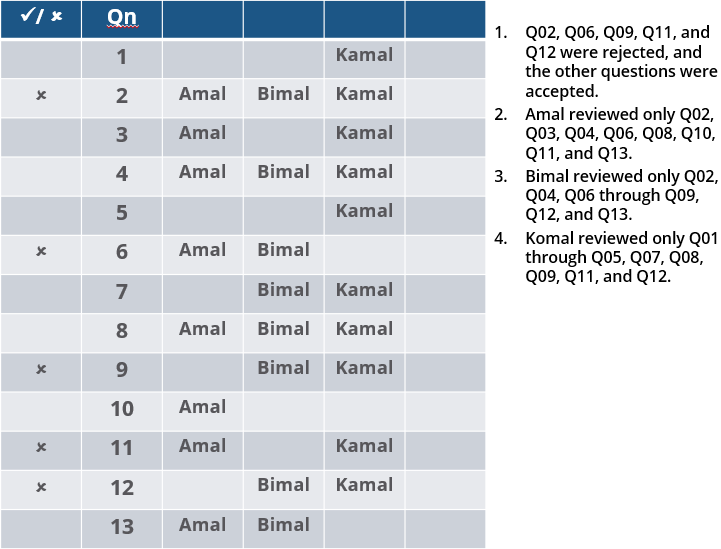
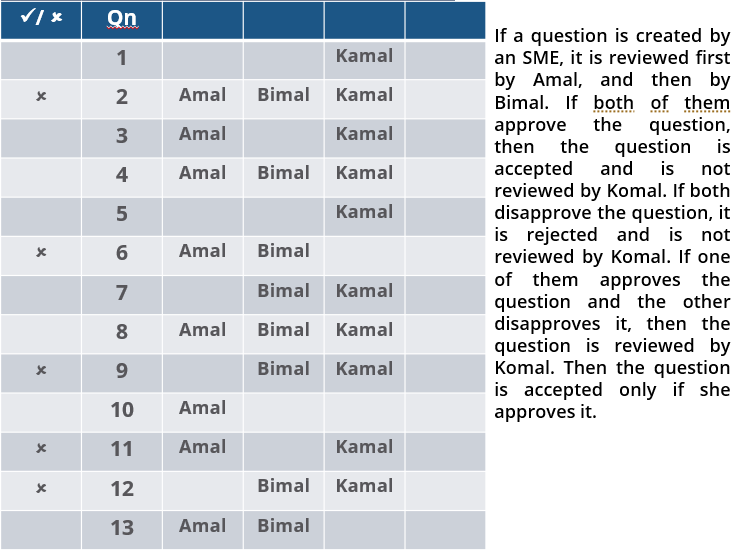
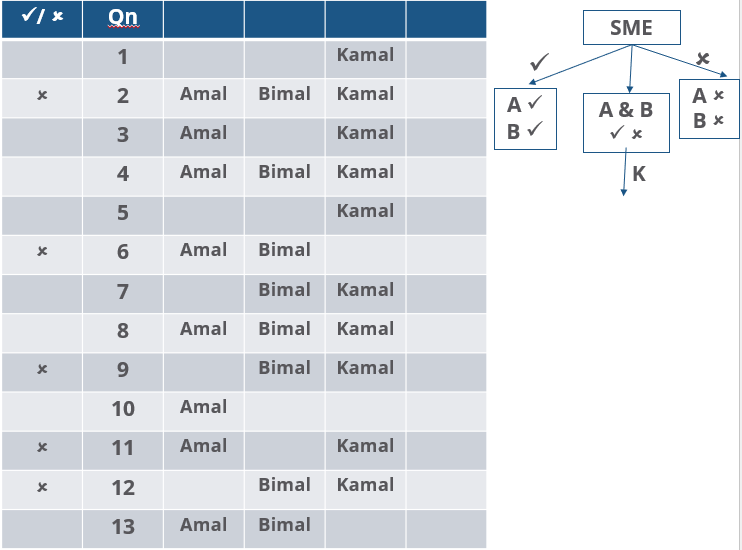
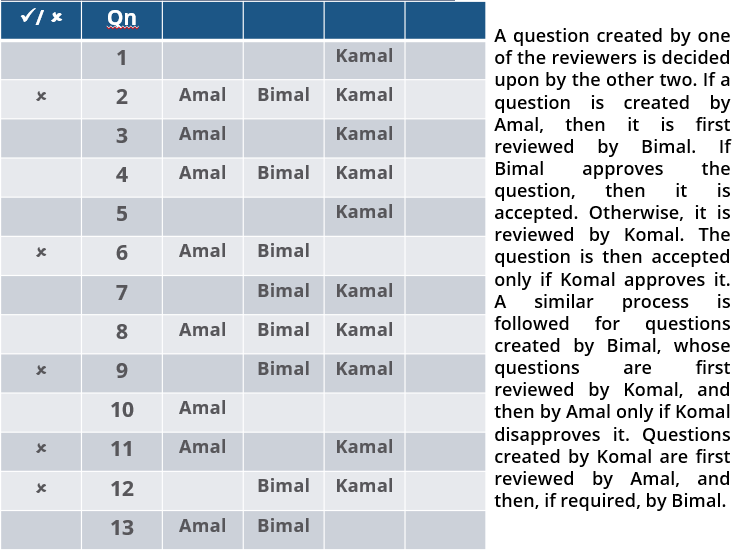
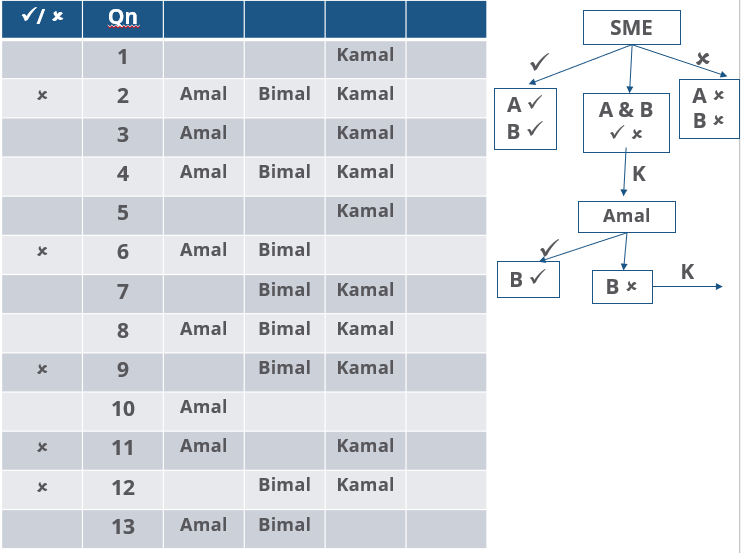
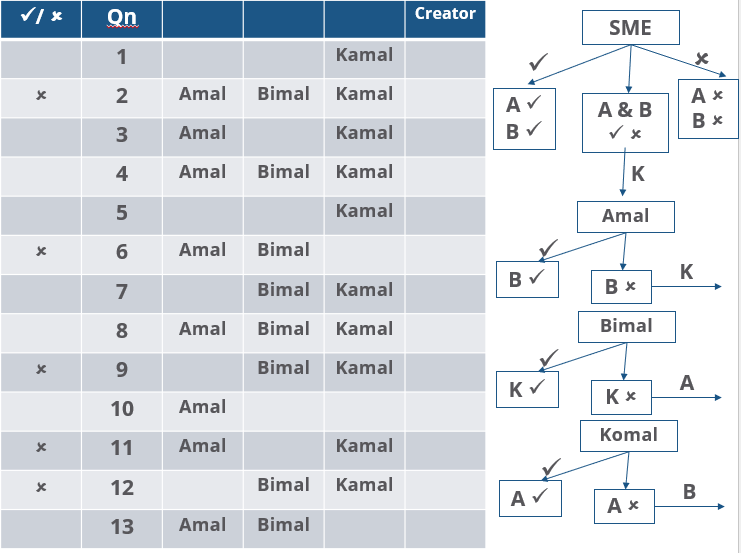
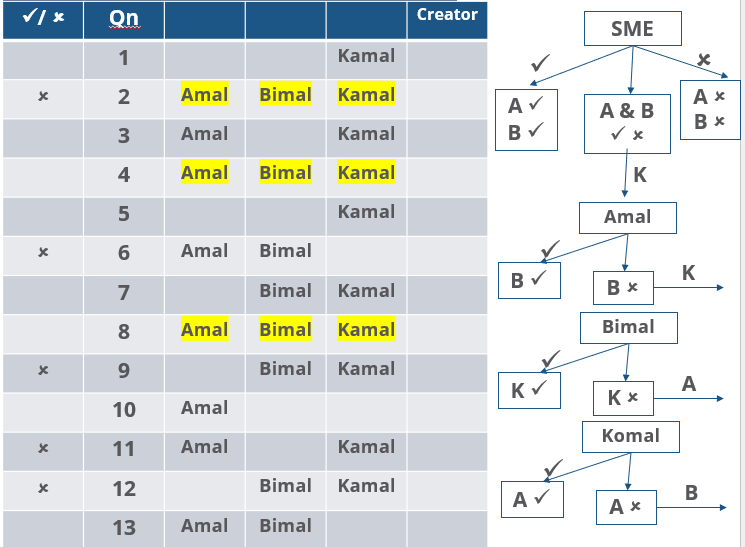
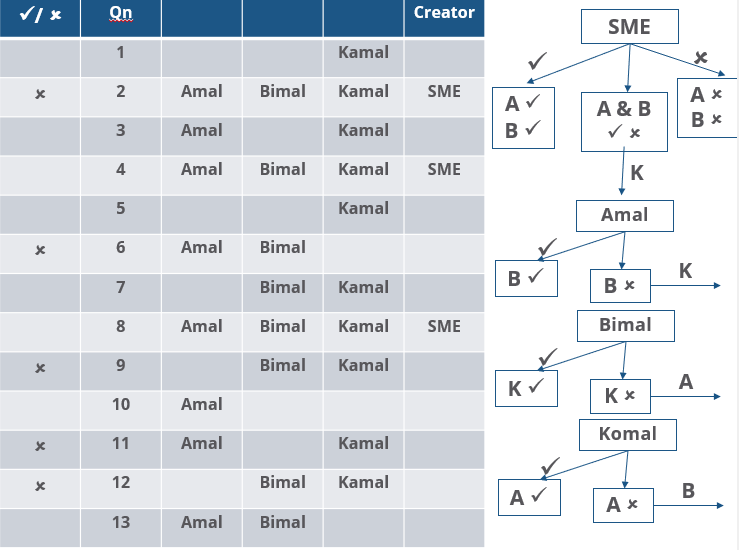
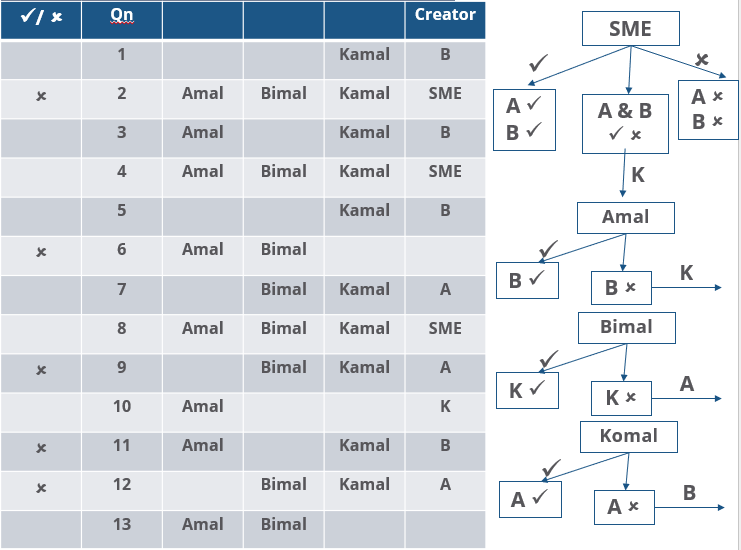
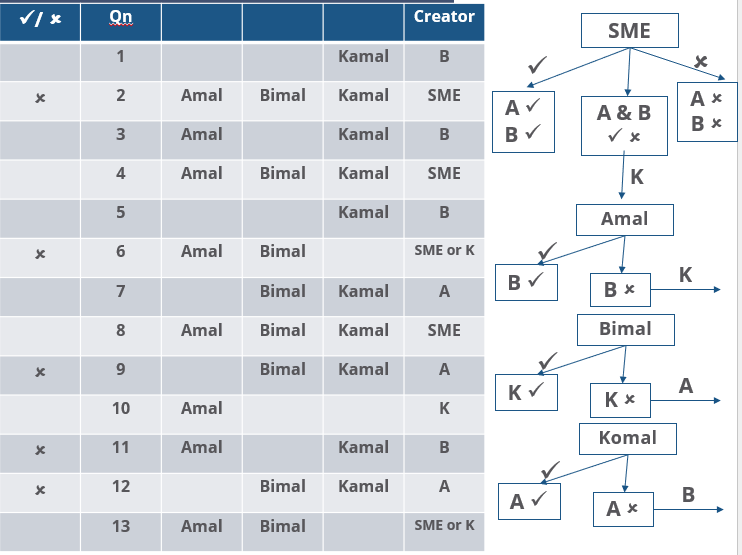
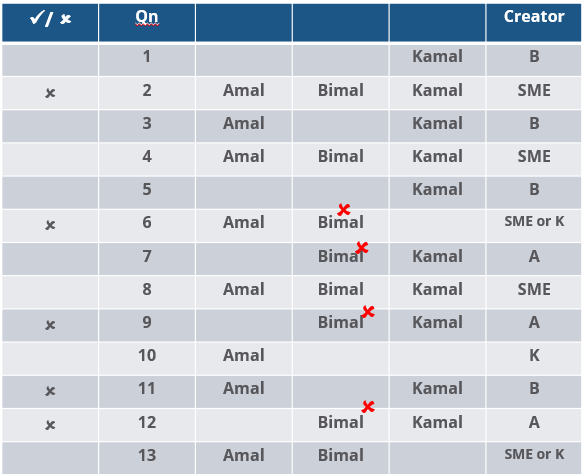
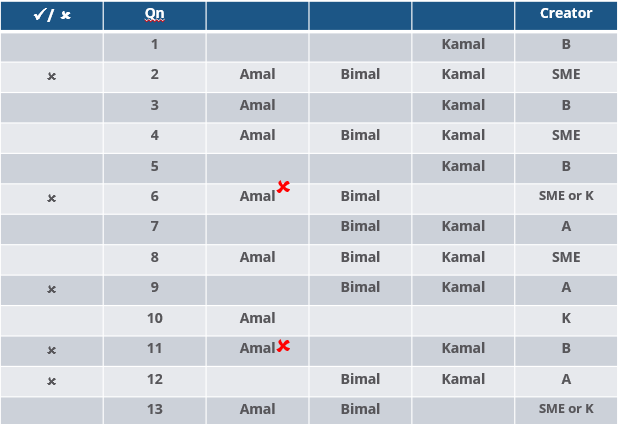
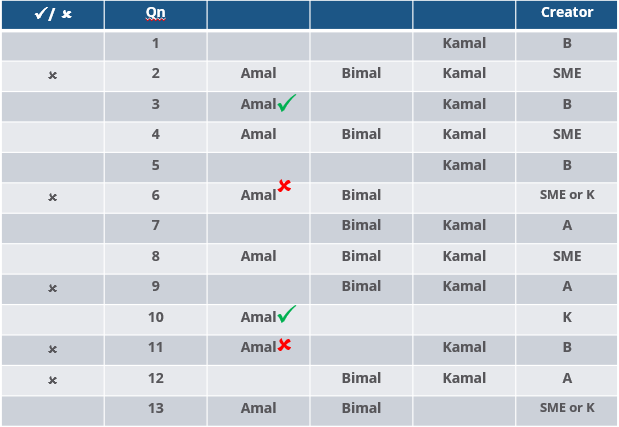
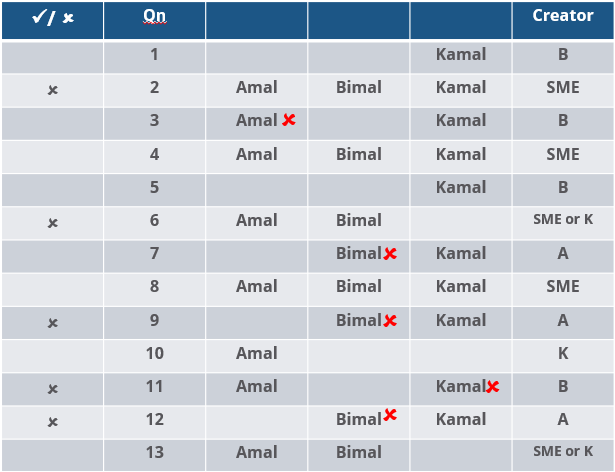
    Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external "subject matter experts" (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
     
    If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
     
    A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
     
    The following facts are known about the review process after its completion.
     
    1. Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted. 
    2. Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
    3. Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
    4. Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.

     

     

    01.

    How many questions were DEFINITELY created by Komal?
    Answer : 1

    Video Explanation

    Explanatory Answer

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    02.

    How many questions were DEFINITELY created by the SMEs?
    Answer : 3

    Video Explanation

    Explanatory Answer

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    03.

    How many questions were DEFINITELY disapproved by Bimal?
    Option C is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    04.

    The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal's approval ratio?
    Option A is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    05.

    How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
    Option A is the correct answer.

    Video Explanation

    Explanatory Answer

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    Set 1

    05.

    Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is
    Answer : The answer is '3000'

    Video Explanation

    Explanatory Answer

    06.

    A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
    Answer : The answer is '3500'

    Video Explanation

    Explanatory Answer

    The are of the rhombus is given by,
    Area = ½ × d1 × d2
    Where d1 & d2 are the diagonals of the rhombus.
    Rhombus of side 10
    Area = ½ × d1 × d2
    96 = ½ × d1 × d2
    96 × 4 = 2 × d1 × d2
    Also,

    d12 + d22 = 400
    (d1 + d2 )2 = d12 + d22 + 2 × d1 × d2
    (d1 + d2 )2 = 400 + 4(96)
    (d1 + d2 )2 = 4(100 + 96)
    (d1 + d2 )2 = 4(196)
    (d1 + d2) = 2(14)
    d1 + d2 = 28
    The cost of laying electric wires along the diagonals at the rate of ₹125 per meter
    = 28 × 125
    = ₹3500

    07.

    The number of distinct pairs of integers (m,n) satisfying |1+mn| < |m + n| < 5 is
    Answer : The answer is '12'

    Video Explanation

    Explanatory Answer

    |1 + mn| < |m + n| < 5
    For two numbers ‘a’ and ‘b’,
    |a| < |b| is equivalent to a2 < b2


    So, we can say that:
    (1 + mn)2 < (m + n)2
    1 + 2mn +m2n2 < m2 + n2 + 2mn
    1 - n2 - m2 + m2n2 < 0
    (1 - n2) - m2(1 - n2) < 0
    (1 - m2)(1 - n2) < 0


    For the product to be negative, either one of the two terms has to be negative.
    But they cannot simultaneously be 0.
    The only possibility for either of the two terms to be positive is when
    n = 0 and |m| > 1, or |n| > 1 and m = 0


    Now for the case when m = 0 and |n| > 1
    |m + n| < 5
    |0 + n| < 5
    So n can be ±±2, ±±3, ±±4
    Which are 6 cases

    Similarly for the case when n = 1 and |m| > 1
    |m + n| < 5
    |0 + m| < 5
    So m can be ±±2, ±±3, ±±4
    Again we have 6 cases.
    Hence the answer is 12.

    08.

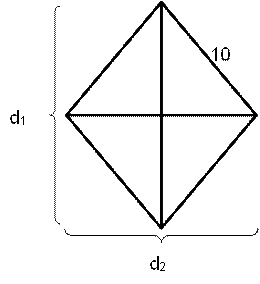
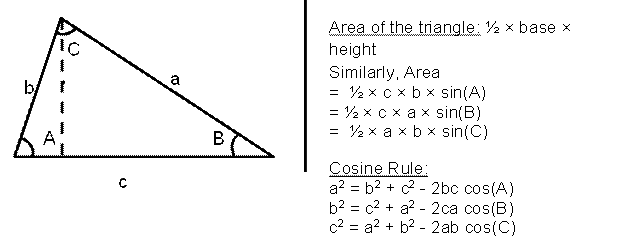
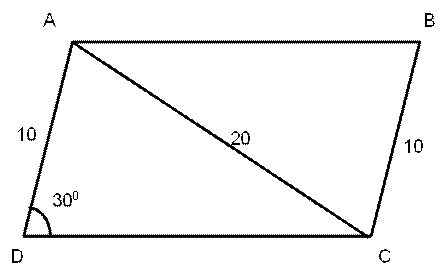
    Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle ∠ADC is equal to 30° then the area of the parallelogram, in sq. cm, is
    Option B is the correct answer.

    Video Explanation

    Explanatory Answer

    Revising the Cosine rule and the area of the triangle using the Sine rule…
    Explanation of the sine and cosine rules
    We draw the described parallelogram ABCD.
    Parallelogram ABCD

    09.

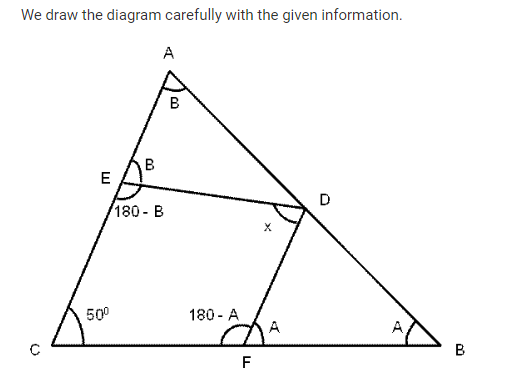
    In a triangle ABC, ∠ BCA = 50°. D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF, then ∠FDE, in degrees, is equal to 
    Option B is the correct answer.

    Video Explanation

    Explanatory Answer

    From the triangle ABC,
    ∠A + ∠B + ∠C = 1800
    ∠A + ∠B + 500 = 1800
    ∠A + ∠B = 1300
    In the quadrilateral CFDE,
    ∠C + ∠F + ∠D + ∠E = 3600
    500 + 1800 - ∠A + ∠x + 1800 - ∠B = 3600
    500 + ∠x = ∠A + ∠B
    500 + ∠x = 1300
    ∠x = 800
    ∠FDE = 800

    10.

    A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
    Answer : The answer is '50'

    Video Explanation

    Explanatory Answer

    We will select the 4 digits first and arrange them later.
    Out of the 4 digits, one of them should be 2 and one of them should be 3.
    2, 3, , .
    So, we just need to select the other two digits…
    The two digits could be (1,1), (2, 2), (3, 3), (1, 2), (1, 3), or (2, 3).
    So, the selection of numbers could be…
    2, 3, 1, 1
    2, 3, 2, 2
    2, 3, 3, 3
    2, 3, 1, 2
    2, 3, 1, 3
    2, 3, 2, 3
    Each of these selections could be re-arranged in a number of ways.

    So total number of possibilities = (12 + 4 + 4 + 12 + 12 + 6) = 50 ways.
    Alternate method:
    (Arrangements with at least one 2 and one 3) = (All possible arrangements) - (Arrangements with either 1 or 2) - (Arrangements with either 1 or 3) + (Arrangements with only 1)
    Think why we need to add (Arrangements with only 1)!

    _, _, _, _
    (All possible arrangements) = 34
    Each blank could be any one of 1, 2 or 3.
    (Arrangements with either 1 or 2) = 24
    Each blank could be any one of 1 or 2.
    (Arrangements with either 1 or 3) = 24
    Each blank could be any one of 1 or 3.
    (Arrangements with only 1) = 1
    Each blank is filled with 1.
    (Arrangements with at least one 2 and one 3) = (All possible arrangements) - (Arrangements with either 1 or 2) - (Arrangements with either 1 or 3) + (Arrangements with only 1)
    (Arrangements with at least one 2 and one 3) = 34 - 24 - 24 + 1
    (Arrangements with at least one 2 and one 3) = 81 - 16 - 16 + 1
    (Arrangements with at least one 2 and one 3) = 82 - 32 = 50