Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
13.2K
Learners
asked the doubt
Previous Year Questions
Revenue & Cost
A large store has only three departments, Clothing, Produce, and Electronics. The following figure shows the percentages of revenue and cost from the three departments for the years 2016, 2017 and 2018. The dotted lines depict percentage levels. So for example, in 2016, 50% of store's revenue came from its Electronics department while 40% of its costs were incurred in the Produce department.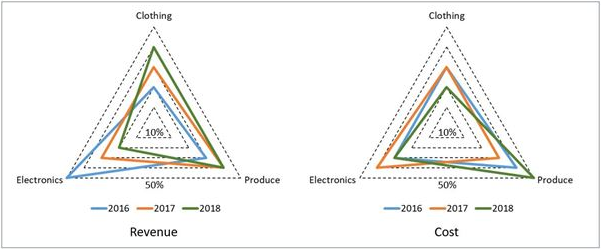
In this setup, Profit is computed as (Revenue – Cost) and Percentage Profit as Profit/Cost × 100%.
It is known that
1. The percentage profit for the store in 2016 was 100%.
2. The store’s revenue doubled from 2016 to 2017, and its cost doubled from 2016 to 2018.
3. There was no profit from the Electronics department in 2017.
4. In 2018, the revenue from the Clothing department was the same as the cost incurred in the Produce department.
What was the percentage profit of the store in 2018? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Percentage profit of the store in 2018= 50/200 = 25%
What was the ratio of revenue generated from the Produce department In 2017 to that in 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
The ratio of the revenues =160 :100 = 8 :5
What percentage of the total profits for the store in 2016 was from the Electronics department? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Profit of the store from the Electronics department in 2016 =100 -30 = 70
Total profit =100 The required percentage = 70%.
What was the approximate difference in profit percentages of the store in 2017 and 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Profit percentage of the store in 2017 =100 /300 =33.3%
Profit percentage of the store in 2018 = 50/200 = 25.0%
The required difference 33.3- 25.0 8.3
MT & ET
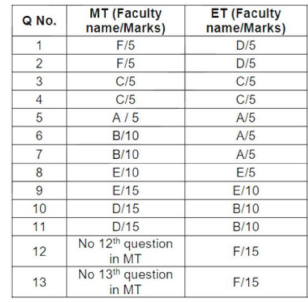
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
The second question in ET was prepared by:
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
How many 5‐mark questions were there in MT and ET combined?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Who prepared 15-mark questions for MT and ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Which of the following questions did Beti prepare in ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
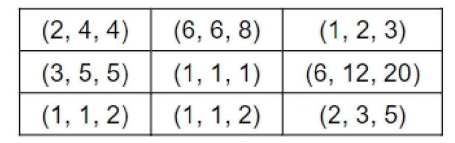
Three pouches
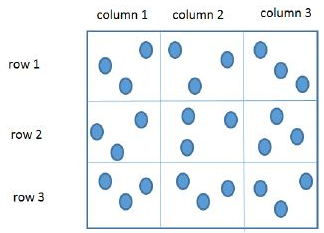
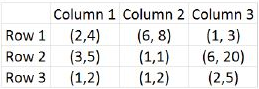
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8.
There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
How many pouches contain exactly one coin? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
What is the number of slots for which the average amount (in rupees) of its three pouches is an integer? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
In three slots (row 2 , column 1), (row 1 , column 2) and (row 2, column 3), the amount in
the three pouches strictly exceeds 10
Three doctors
Three doctors, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges Rs. 100/-. Dr. Kane sees each patient for 15 minutes and charges Rs. 200/-, while Dr. Wayne sees each patient for 25 minutes and charges Rs. 300/-. The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.
The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday. On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
What is the maximum number of patients that the clinic can cater to on any single day?
Video Explanation
The queue is never empty on one particular Saturday. Which of the three doctors would earn the maximum amount in consultation charges on that day?
Video Explanation
Mr. Singh visited the clinic on Monday, Wednesday, and Friday of a particular week, arriving at 8:50 a.m. on each of the three days. His token number was 13 on all three days. On which day was he at the clinic for the maximum duration?
Video Explanation
Explanatory Answer
Mr. Singh takes maximum duration when he enters Dr. Wayne’s room, who sees each
patient for 25 minutes
He was at the clinic for 85 minutes.
Similarly On Wednesday, he would meet Ben and he would be at the clinic for 70 minutes.
On Friday, he would meet Ben and he would be at the clinic for 70 minutes.
Therefore, Singh stays at the clinic for the maximum duration on Monday
Ans: (Monday)
On a slow Thursday, only two patients are waiting at 9 a.m. After that two patients keep arriving at exact 15 minute intervals starting at 9:15 a.m. -- i.e. at 9:15 a.m., 9:30 a.m., 9:45 a.m. etc. Then the total duration in minutes when all three doctors are simultaneously free is
Video Explanation
Explanatory Answer
The above pattern continues.
Hence, there is no time where all the doctors are simultaneously free.
Ans: (0)
Students & Proposals
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates.
A survey was conducted among the students by picking a sample of 500 students. The following information was noted from this survey.
1) 250 students supported proposal A and 250 students supported proposal B.
2) Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3) Among those who preferred Ragini, 30% supported proposal A.
4) 20% of those who supported proposal B preferred Sunita.
5) 40% of those who did not support proposal B preferred Ragini.
6) Every student who preferred Sunita and supported proposal B also supported proposal A.
7) Among those who preferred Ragini, 20% did not support any of the proposals.
Among the students surveyed who supported proposal A, what percentage preferred Sunita for student union president? [TITA]
Video Explanation
Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows
There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.
The required value is 160/250*100 = 64
What percentage of the students surveyed who did not support proposal A preferred Ragini as student union president? [TITA]
Video Explanation
Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows
There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.
The required answer is 210/250*100 = 84
What percentage of the students surveyed who supported both proposals A and B preferred Sunita as student union president?
Video Explanation
Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows
There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.
The required answer is 50/250*100 = 50
How many of the students surveyed supported proposal B, did not support proposal A and preferred Ragini as student union president?
Video Explanation
Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows
There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.
The students who supported proposal B but not A are b (Sunita) and b (Ragini). Among
them those supported Ragini are b (Ragini) 150. Ans: (150)
Rainfall
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.
If a ‘Heavy Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 900 mm or more, then approximately what percentage of ‘Heavy Monsoon States’ have a negative deviation from respective LPAs in 2019?
Video Explanation
Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.
The heavy monsoon states are Maharashtra, Sikkim, Mizoram, Goa, Arunachal, Kerala and
Meghalaya. Among these, Arunachal, Kerala and Meghalaya have a negative deviation from
respective LPAs in 2019. The required percentage = 3/7*100 = 42.86
If a ‘Low Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 750 mm or less, then what is the median ‘deviation from LPA’ (as defined in the Y-axis of the figure) of ‘Low Monsoon States’?
Video Explanation
Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.
The Low monsoon states are Gujarat, Karnataka, Rajasthan, MP, Assam, WB, Jharkhand,
Delhi and Manipur. The deviation from LPA for these states are 25,20,15, 10,-10,-30,-35,-40
and -60. The median value is -10
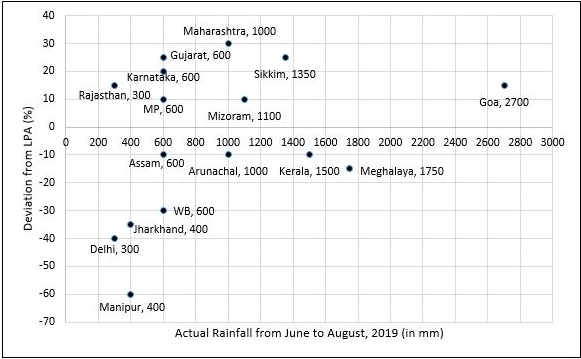
What is the average rainfall of all states that have actual rainfall of 600 mm or less in 2019 and have a negative deviation from LPA?
Video Explanation
Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.
The states which have a negative deviation from LPA and have an actual rainfall of 600 mm
or less are Assam, WB, Jharkhand, Delhi and Manipur. The average rainfall in these states is
2300/5 = 460 mm
The LPA of a state for a year is defined as the average rainfall in the preceding 10 years considering the period of June-August. For example, LPA in 2018 is the average rainfall during 2009-2018 and LPA in 2019 is the average rainfall during 2010-2019. It is also observed that the actual rainfall in Gujarat in 2019 is 20% more than the rainfall in 2009. The LPA of Gujarat in 2019 is closest to
Video Explanation
Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.
The actual rainfall in Gujarat in 2019 is 600 mm. The rainfall in Gujarat in 2009 was 500 mm.
As the value of 500 is replaced by 600 in calculating the LPA, the LPA would increase by 10
as it is the average of 10 years.
Ans: (490 mm)
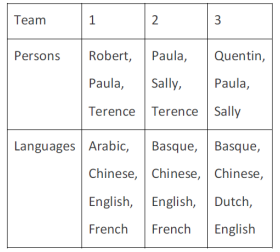
Languages spoken
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally and Terence. For example, Paula speaks only Chinese and English.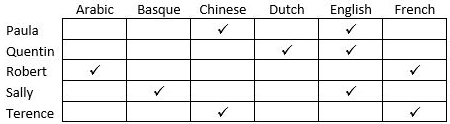
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Who among the following four is not a member of Team 2?
Video Explanation
Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.
Who among the following four people is a part of exactly two teams?
Video Explanation
Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.
Who among the five people is a member of all teams?
Video Explanation
Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.
Apart from Chinese and English, which languages are spoken by Team 1?
Video Explanation
Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.
A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively. Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x - y) / p equals
Video Explanation
Amal invests Rs 12000 at 8% interest, compounded annually, and Rs 10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is
Video Explanation
Explanatory Answer
Previous year papers
2024
2023
2022
2021
2020
2019
2018