Started 3 weeks ago by Sarthak Ahire in
A can do a piece of work in 10 days working 8 hours per day. If B is two-thirds as efficient as A, then in how many days can B alone do the same piece of working working 5 hours per day?
Body
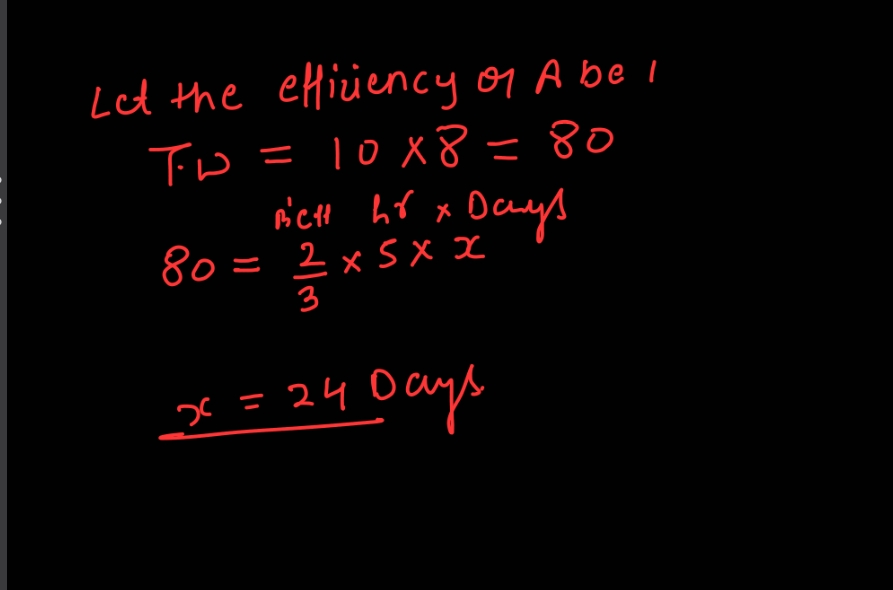
8 Replies
-
Replied 8 months ago
To solve this problem, we need to first determine the total amount of work in terms of hours and then calculate how long it will take B to complete the same work given his efficiency and hours per day. Determine the Total Work A Does: A can complete the work in 10 days working 8 hours per day. Total work done by A = 10 days × 8 hours/day = 80 hours. Determine B's Efficiency: B is two-thirds as efficient as A. This means if A does 1 unit of work in an hour, B does ( \frac{2}{3} ) of that work in an hour. Calculate the Time B Takes to Complete the Work: If A takes 80 hours to complete the work, B will take (\frac{80}{\frac{2}{3}}) hours to do the same work because he is two-thirds as efficient. Calculating (\frac{80}{\frac{2}{3}} = 80 \times \frac{3}{2} = 120 ) hours. Therefore, B needs 120 working hours to complete the same work. Calculate the Number of Days Required for B: B works 5 hours per day. Number of days B needs = ( \frac{120 \text{ hours}}{5 \text{ hours/day}} = 24 \text{ days} ). So, B can complete the work in 24 days working 5 hours per day.
Replied 8 months ago
To solve this problem, we need to first determine the total amount of work in terms of hours and then calculate how long it will take B to complete the same work given his efficiency and hours per day. Determine the Total Work A Does: A can complete the work in 10 days working 8 hours per day. Total work done by A = 10 days × 8 hours/day = 80 hours. Determine B's Efficiency: B is two-thirds as efficient as A. This means if A does 1 unit of work in an hour, B does ( \frac{2}{3} ) of that work in an hour. Calculate the Time B Takes to Complete the Work: If A takes 80 hours to complete the work, B will take (\frac{80}{\frac{2}{3}}) hours to do the same work because he is two-thirds as efficient. Calculating (\frac{80}{\frac{2}{3}} = 80 \times \frac{3}{2} = 120 ) hours. Therefore, B needs 120 working hours to complete the same work. Calculate the Number of Days Required for B: B works 5 hours per day. Number of days B needs = ( \frac{120 \text{ hours}}{5 \text{ hours/day}} = 24 \text{ days} ). So, B can complete the work in 24 days working 5 hours per day.
Replied 8 months ago
SmartSelect_20241215_130530_Samsung Notes.jpg 73.75 KB
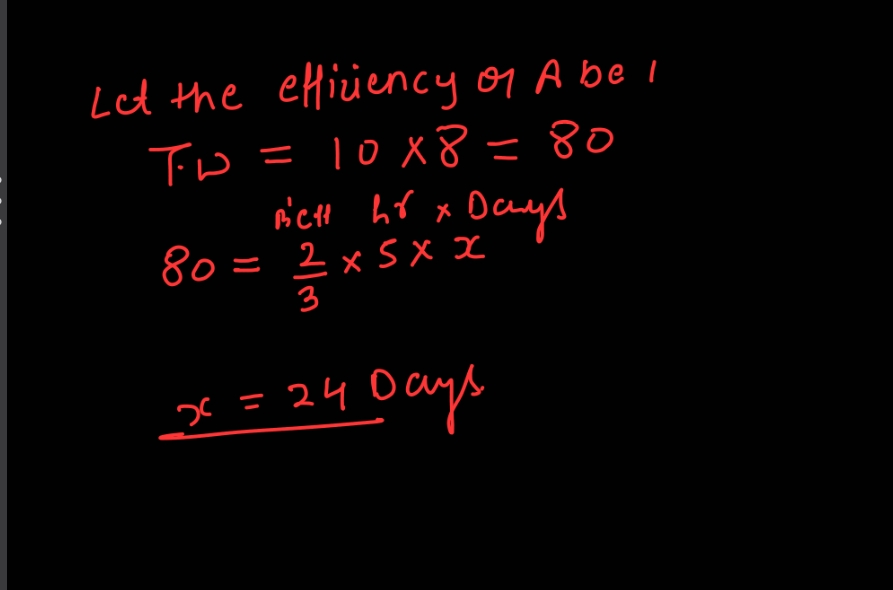
Replied 8 months ago
SmartSelect_20241215_130530_Samsung Notes.jpg 73.75 KB
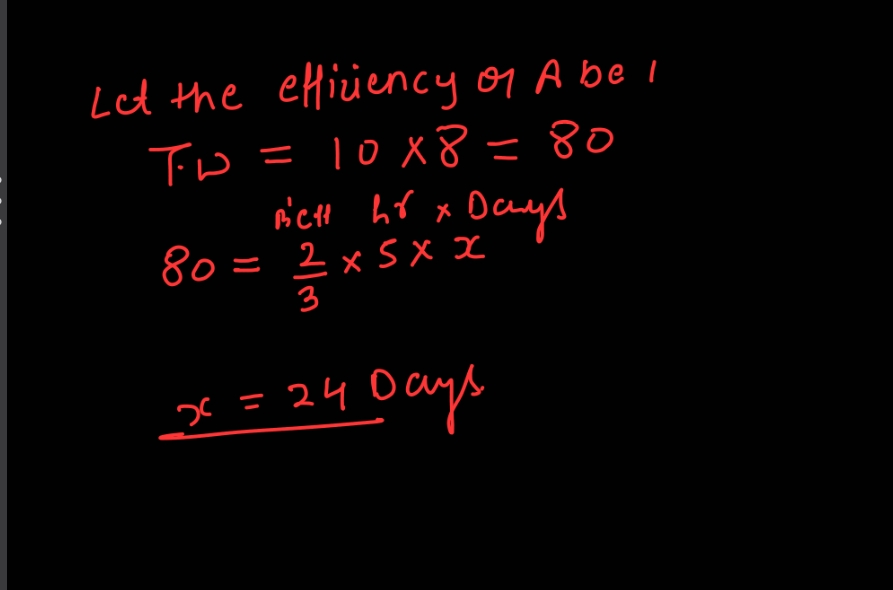
Replied 3 weeks ago
How to solve in the fastest way possible in terms of CET exam. A can do a piece of work in 10 days working 8 hours per day. If B is two-thirds as efficient as A, then in how many days can B alone do the same piece of working working 5 hours per day?
Replied 3 weeks ago
How to solve in the fastest way possible in terms of CET exam. A can do a piece of work in 10 days working 8 hours per day. If B is two-thirds as efficient as A, then in how many days can B alone do the same piece of working working 5 hours per day?
Replied 3 weeks ago
How to solve in the fastest way possible in terms of CET exam. A can do a piece of work in 10 days working 8 hours per day. If B is two-thirds as efficient as A, then in how many days can B alone do the same piece of working working 5 hours per day?
