Started 3 weeks ago by Shubham Kumar Singh in
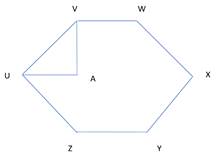
In the figure below, UVWXYZ is a regular hexagon and ∠ VAU = 120°. Find the ratio of area of triangle AVU to the regular hexagon?
Body
3 Replies
-
Replied 10 months ago
If VAU = 120 degrees and VA is vertical, we can say that angle AVU = angle AUV = 30 degrees.Now, considering the side of the regular hexagon to be 2a units, we get UA = 2a / sqrt(3) = AVNow, area of AUV = 1/2 * 2a * a/2 = a^2 / 2and area of UVWXYZ = 3 * sqrt(3) * (2a)^2 / 2 = 6 * sqrt(3) * a^2Now, the required ratio is 1 : 12 * sqrt(3)
Replied 3 weeks ago
In the figure below, UVWXYZ is a regular hexagon and ∠ VAU = 120°. Find the ratio of area of triangle AVU to the regular hexagon? In the figure below, UVWXYZ is a regular hexagon and ∠ VAU = 120°. Find the ratio of area of triangle AVU to the regular hexagon?

