The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Started 1 month ago by Shashank in
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
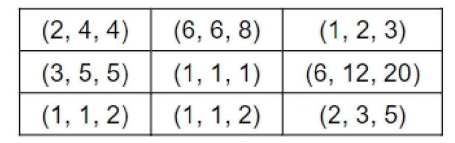
In three slots (row 2 , column 1), (row 1 , column 2) and (row 2, column 3), the amount in
the three pouches strictly exceeds 10
-
No one is replied to this question yet. Be first to reply!
