Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
After two successive increments, Gopal's salary became 187.5% of his initial salary. If the percentage of
salary increase in the second increment was twice of that in the first increment, then the percentage of
salary increase in the first increment was
Video Explanation

The number of all positive integers up to 500 with non-repeating digits is
Video Explanation

Rajesh and Vimal own 20 hectares and 30 hectares of agricultural land, respectively, which are entirely
covered by wheat and mustard crops. The cultivation area of wheat and mustard in the land owned by
Vimal are in the ratio of 5 : 3. If the total cultivation area of wheat and mustard are in the ratio 11 : 9, then
the ratio of cultivation area of wheat and mustard in the land owned by Rajesh is
Video Explanation

For some constant real numbers p, k and a, consider the following system of linear equations in x and y:
px - 4y = 2
3x + ky= a
A necessary condition for the system to have no solution for (x, y ), is
Video Explanation

For any non-zero real number x, let f(x)+2f(1/x)=3x. Then, the sum of all possible values of x for which f(x)=3, is
Video Explanation

The number of distinct integer solutions (x,y) of the equation |x+y|+|x−y|=2, is
Video Explanation

A regular octagon ABCDEFGH has sides of length 6 cm each. Then the area, in sq. cm, of the square ACEG
is
Video Explanation

f 3^a=4,4^b=5,5^c=6,6^d=7,7^e=8 and 8^f=9, then the value of the product abcdef is
Video Explanation

The sum of all distinct real values of x that satisfy the equation 10^x+4/10^x=81/2, is
Video Explanation

The number of distinct real values of x, satisfying the equation max{x,2}−min{x,2}=|x+2|−|x−2|, is
Video Explanation

Question:
Consider the sequence t1 = 1, t2 = -1 and tn = ((n-3)/(n-1)) * t(n-2) for n ≥ 3.
Then, the value of the sum
1/t2 + 1/t4 + 1/t6 + ... + 1/t2022 + 1/t2024
is ____.
Video Explanation

Sam can complete a job in 20 days when working alone. Mohit is twice as fast as Sam and thrice as fast as
Ayna in the same job. They undertake a job with an arrangement where Sam and Mohit work together on
the first day, Sam and Ayna on the second day, Mohit and Ayna on the third day, and this three-day pattern is
repeated till the work gets completed. Then, the fraction of total work done by Sam is
Video Explanation

If (a+b√3)^2=52+30√3, where a and b are natural numbers, then a+b equals
Video Explanation

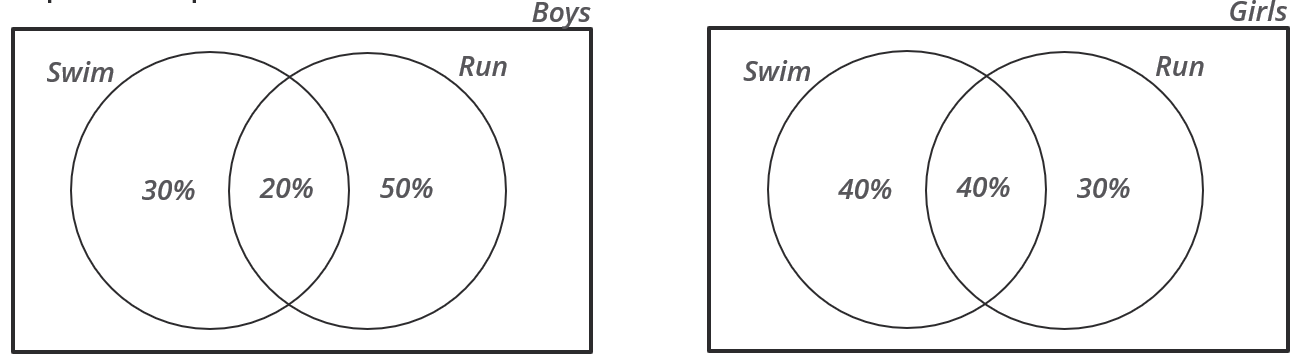
In a group of 250 students, the percentage of girls was at least 44% and at most 60%.The rest of the
students were boys. Each student opted for either swimming or running or both. If 50% of the boys and 80%
of the girls opted for swimming while 70%of the boys and 60% of the girls opted for running, then the
minimum and maximum possible number of students who opted for both swimming and running, are
Video Explanation

What best can be concluded about the number of times the AC must have either been turned on or the AC
temperature setting been altered between 11:01 pm and 1:59 am?
Video Explanation

What was the temperature outside, in degree Celsius, at 9 pm?
Video Explanation

What was the temperature outside, in degree Celsius, at 1 am?
Video Explanation

How many times the AC must have been turned off between 11:01 pm and 1:59 am?
Video Explanation

The air-conditioner (AC) in a large room can be operated either in REGULAR mode or in POWER mode to reduce
the temperature.
If the AC operates in REGULAR mode, then it brings down the temperature inside the room(called inside
temperature) at a constant rate to the set temperature in 1 hour. If it operates in POWER mode, then this is
achieved in 30 minutes.
If the AC is switched off, then the inside temperature rises at a constant rate so as to reach the temperature
outside at the time of switching off in 1 hour.
The temperature outside has been falling at a constant rate from 7 pm onward until 3 am on a particular night.
The following graph shows the inside temperature between 11 pm (23:00)and 2 am (2:00) that night.
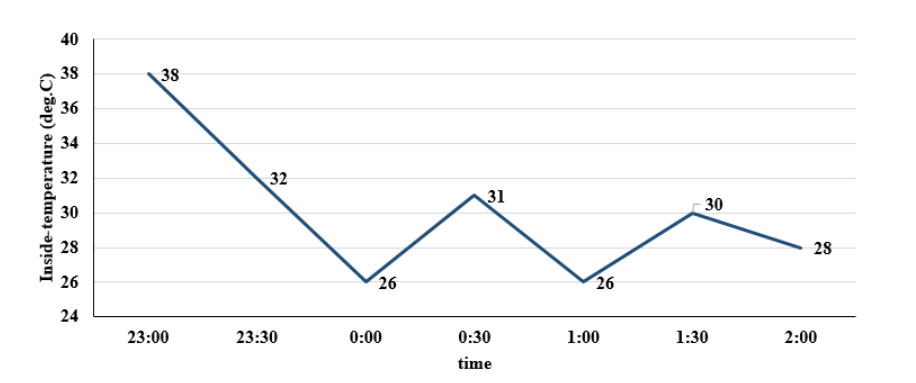
The following facts are known about the AC operation that night.
• The AC was turned on for the first time that night at 11 pm (23:00).
• The AC setting was changed (including turning it on/off, and/or setting different temperatures) only at the
beginning of the hour or at 30 minutes after the hour.
• The AC was used in POWER mode for longer duration than in REGULAR mode during this 3-hour period.
How many times the AC must have been turned off between 11:01 pm and 1:59 am?
Video Explanation

What was the temperature outside, in degree Celsius, at 1 am?
Video Explanation

What was the temperature outside, in degree Celsius, at 9 pm?
Video Explanation

What best can be concluded about the number of times the AC must have either been turned on or the AC
temperature setting been altered between 11:01 pm and 1:59 am?
Video Explanation

For how many countries among Country 1 through Country 8 will the GDP per capita in 2027 be lower than
that in 2024?
Video Explanation

Which one among the countries 1, 4, 5, and 7 will have the largest population in 2027?
Video Explanation

Which one among the countries 1 through 8, has the smallest population in 2024?
Video Explanation

The ratio of Country 4’s GDP to Country 5’s GDP in 2026 will be closest to
Video Explanation

Out of 10 countries -- Country 1 through Country 10 -- Country 9 has the highest gross domestic product (GDP),
and Country 10 has the highest GDP per capita. GDP per capita is the GDP of a country divided by its
population. The table below provides the following data about Country 1 through Country 8 for the year 2024.
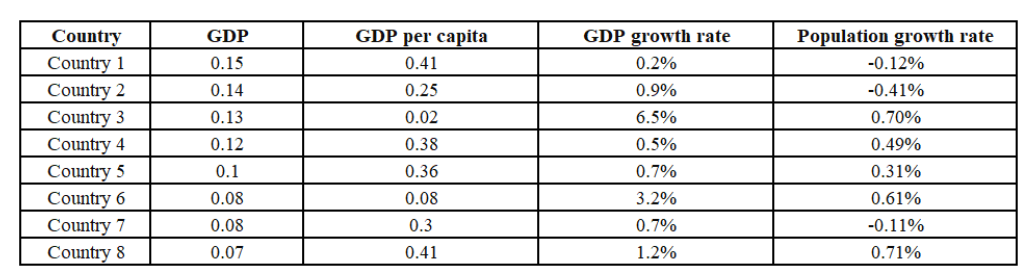
• Column 1 gives the country's identity.
• Column 2 gives the country’s GDP as a fraction of the GDP of Country 9.
• Column 3 gives the country’s GDP per capita as a fraction of the GDP per capita of Country10.
• Column 4 gives the country’s annual GDP growth rate.
• Column 5 gives the country’s annual population growth rate.
Assume that the GDP growth rates and population growth rates of the countries will remain constant for the
next three years
Which one among the countries 1 through 8, has the smallest population in 2024?
Video Explanation

The ratio of Country 4’s GDP to Country 5’s GDP in 2026 will be closest to
Video Explanation

Which one among the countries 1, 4, 5, and 7 will have the largest population in 2027?
Video Explanation

For how many countries among Country 1 through Country 8 will the GDP per capita in 2027 be lower than
that in 2024?
Video Explanation

What could be the minimum percentage of subscribers who used multiple apps in 2024?
Video Explanation

What was the percentage increase in the number of subscribers in the ‘Elder’ categoryfrom 2023 to 2024?
Video Explanation

What percentage of subscribers in the ‘Kid’ category used multiple apps in 2023?
Video Explanation

How many subscribers belonged to the ‘Others’ category in 2024?
Video Explanation

Comprehension:
Over the top (OTT) subscribers of a platform are segregated into three categories: i) Kid, ii)Elder, and iii) Others.
Some of the subscribers used one app and the others used multiple apps to access the platform. The figure
below shows the percentage of the total number of subscribers in 2023 and 2024 who belong to the ‘Kid’ and
‘Elder’ categories.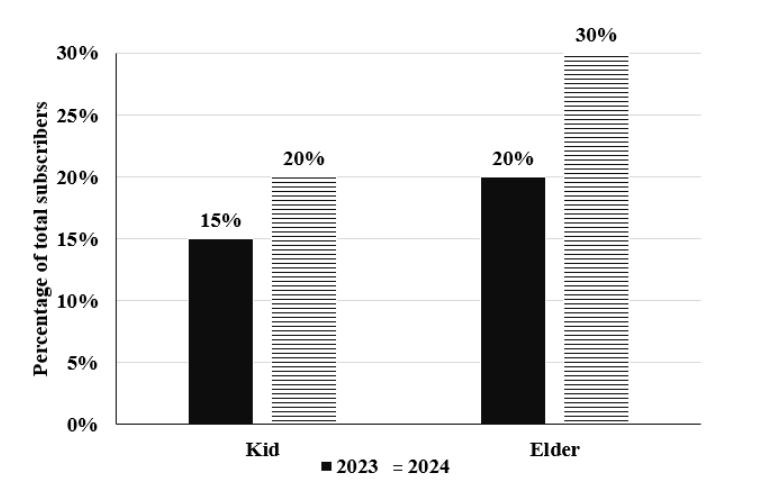
The following additional facts are known about the numbers of subscribers.
1. The total number of subscribers increased by 10% from 2023 to 2024.
2. In 2024, 1/2 of the subscribers from the ‘Kid’ category and 2/3 of the subscribers from the ‘Elder’ category
subscribers use one app.
3. In 2023, the number of subscribers from the ‘Kid’ category who used multiple apps was the same as the
number of subscribers from the ‘Elder’ category who used one app.
4. 10,000 subscribers from the ‘Kid’ category used one app and 15,000 subscribers from the ‘Elder’ category
used multiple apps in 2023.
How many subscribers belonged to the ‘Others’ category in 2024?
Video Explanation

What percentage of subscribers in the ‘Kid’ category used multiple apps in 2023?
Video Explanation

What was the percentage increase in the number of subscribers in the ‘Elder’ categoryfrom 2023 to 2024?
Video Explanation

What could be the minimum percentage of subscribers who used multiple apps in 2024?
Video Explanation

What is the median of the number of grams of protein in 100 grams of nutrients among these food grains?
Video Explanation

How many grams of other nutrients were there in 100 grams of nutrients in M3?
Video Explanation

How many grams of protein were there in 100 grams of nutrients in M2?
Video Explanation

How many foodgrains had a higher amount of carbohydrate per 100 grams ofnutrients than M1?
Video Explanation

The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100
grams of nutrients in seven food grains. The first column shows the food grain category and the second
column its codename. The table has some missing values.
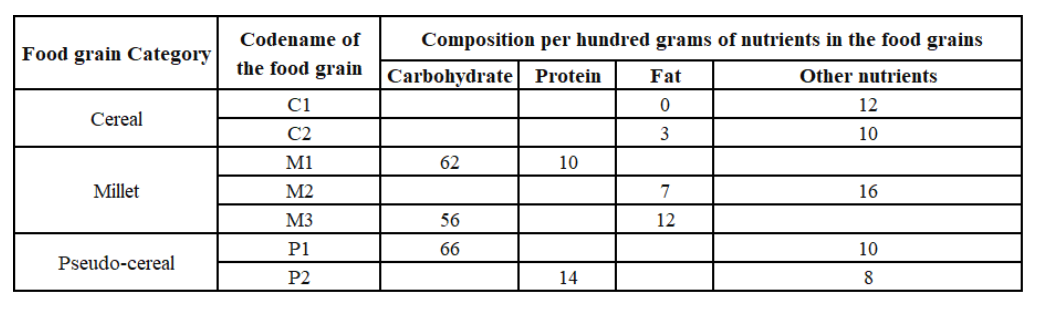
The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any
millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are nonzero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
How many foodgrains had a higher amount of carbohydrate per 100 grams ofnutrients than M1?
Video Explanation

How many grams of protein were there in 100 grams of nutrients in M2?
Video Explanation

How many grams of other nutrients were there in 100 grams of nutrients in M3?
Video Explanation

What is the median of the number of grams of protein in 100 grams of nutrients among these food grains?
Video Explanation

What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
Video Explanation

What best can be said about the road distance (in km) between the ATMs having the second highest and
the second lowest cash requirements?
Video Explanation

How many ATMs have cash requirements of Rs. 10 Lakhs or more?
Video Explanation

The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C
and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance
(in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM
has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure
indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash
requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed
on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the
intersection of R-C and V3 is 12 km.
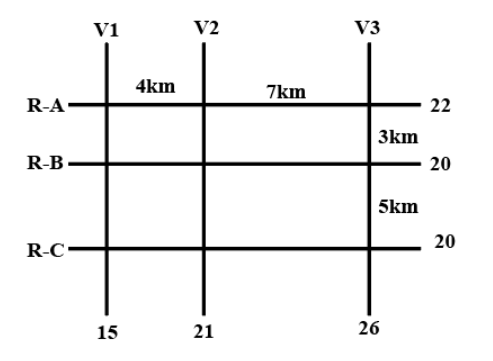
How many ATMs have cash requirements of Rs. 10 Lakhs or more?
Video Explanation

Which of the following two statements is/are DEFINITELY true?
Statement A: Each of R-A, R-B, and R-C has two ATMs.
Statement B: Each of V1, V2, and V3 has two ATMs.
Video Explanation

What best can be said about the road distance (in km) between the ATMs having the second highest and
the second lowest cash requirements?
Video Explanation

What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
Video Explanation

Which of the following two statements is/are DEFINITELY true?
Statement A: Each of R-A, R-B, and R-C has two ATMs.
Statement B: Each of V1, V2, and V3 has two ATMs.
Video Explanation

Question:
The sum of the infinite series
(1/5) * (1/5 - 1/7)
+ (1/5)^2 * ((1/5)^2 - (1/7)^2)
+ (1/5)^3 * ((1/5)^3 - (1/7)^3)
+ ......
is equal to ?
Video Explanation

Previous year papers
2024
2023
2022
2021
2020
2019
2018