Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K? [TITA]
Started 1 year ago by Shashank in
Explanatory Answer
From condition 3, we get the above diagram

Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
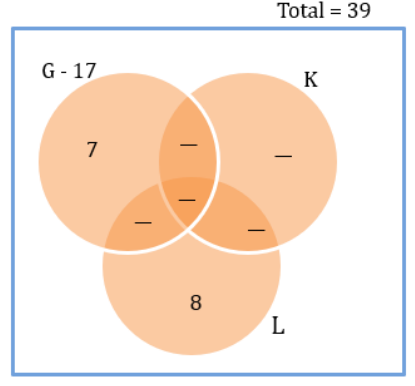
From condition 1, we get the above diagram. 
From condition 6, we can get the diagram.

From condition 4, we get the above diagram.

From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
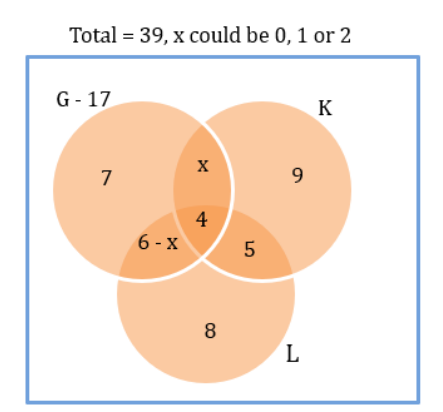
We know that G ∩ K ∩ L = 0. We know that the 4 that were originally here are distributed among
the three regions currently having x, 6 – x and 5.
We know that one student leaves K. So, this student should have gone to the region (G and L but
not K).
Or, (G and L but not K) will now read 7 – x.
The other three should have opted out of one or the other of G and L. Let us assume m students
left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and K = 3 + x – m. 3 + 1 -2 = 2.
-
No one is replied to this question yet. Be first to reply!
Previous year papers
2024
2023
2022
2021
2020
2019
2018

