A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
Started 2 days ago by Shashank in
Explanatory Answer
Since the prices of the small and medium cups are in the ratio 2 : 5,
Let us assume the prices of the small, medium and large cups to be 2x, 5x and y.
We are given that the product of the three prices is 800.
Therefore, (2x)(5x)(y) = 800 —- (1)
If the price of the smallest and the medium cups are increased by 6, then the product becomes 3200
(2x + 6) (5x + 6) (y) = 3200 —- (2)
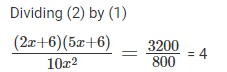
(2x + 6) (5x + 6) = 40 x2
10 x2 + 42x + 36 = 40 x2
30 x2 - 42x - 36 = 0
10 x2 - 14x - 12 = 0
10 x2 - 20x + 6x - 12 = 0
10 x(x - 2) + 6(x - 2) = 0
(10x + 6) (x - 2) = 0
x = 2 or x = -0.6
x can’t be negative and hence x = 2
WKT, (2x)(5x)(y) = 800
(4)(10)(y) = 800
y = 20
Therefore, the sum of the prices = 2x + 5x + y
= 2(2) + 5(2) + 20
= 4 + 10 + 20
= 34
-
No one is replied to this question yet. Be first to reply!
Previous year papers
