CAT 2021 Question Paper | CAT Verbal Ability Slot 1
Question :
Suppose the length of each side of a regular hexagon ABCDEF is 2 cm. If T is the midpoint of CD, then the length of AT, in cm, is
Started 1 month ago by Shashank in
Option A
is the correct answer.
Explanatory Answer
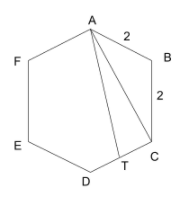
In a regular hexagon, each internal angle is equal to 120°.
From isosceles triangle ABC, we know the length of two sides and including angle.
We will be able to find the third side (AC) using the Pythagoras theorem or the sine rule.
Hence, AC = 2√3cm
Given that, T is the midpoint.
So, CT = 1cm.
From the right-angled △ ACT,
AC2 + CT2 = AT2
AT2 = (2 √3)2 + (1)2 = 13
AT = √(13)
-
No one is replied to this question yet. Be first to reply!
