CAT 2018 Question Paper | CAT Verbal Ability Slot 1
Question :
In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
Started 3 months ago by Shashank in
Option D
is the correct answer.
Explanatory Answer
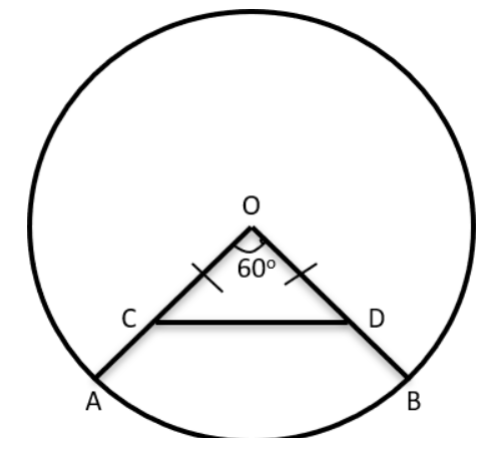
Given ∠AOB = 60°
Area of Sector AOB = 60/360 × π = π/6 ---(1)
Given OC = OD => ∠OCD = ∠ODC = 60°
△OCD is an Equilateral Triangle with side = a
Area(△OCD) = √3/4 × a × a ---(2)
Its given that Area(OCD) = 1/2 × Area(OAB)
a 2 (√3/4) = π / ( 6×2)
a = (π/ 3√3) 1/2
-
No one is replied to this question yet. Be first to reply!
