In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is

CAT 2018 Question Paper | CAT Verbal Ability Slot 1

Question :

Started 3 months ago by Shashank in

0 130

A.
18√3
B.
24√3
C.
32√3
D.
12√3

Option C is the correct answer.

Explanatory Answer

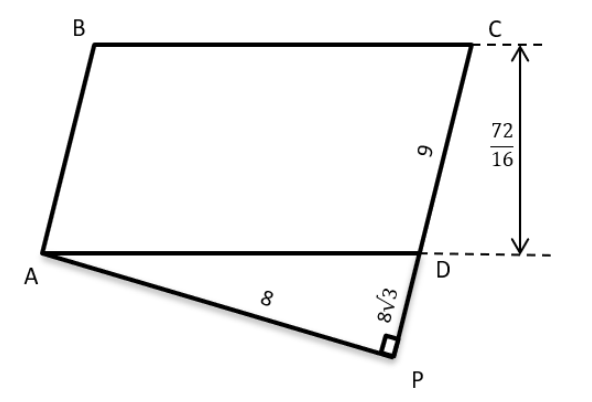
Given Area (ABCD) = 72 sq cm, CD = 9cms, AD = 16cms
Area of Parallelogram = Base × Height
CD × 16 = 72
CD = $\frac{72}{16}$ cms
We extend CD till P such that ∠APD = 90°
So, again by applying the area formula considering CD as base
CD × AP = Area of Parallelogram ABCD
9 × AP = 72
AP = 8 cms

We have AP = 8 cms, AD = 16 cms We observe that the ratio of the sides form a 1 : √3 : 2 triangle Therefore DP = 8√3 cms Area (△APD) = 1/2 × AD × DP = 1/2 × 8 × 8√3 sq cms Area (△APD) = 32 √3 sq cms