A tank is emptied everyday at a fixed time point. Immediately thereafter, either pump A or pump B or both start working until the tank is full. On Monday, A alone completed filling the tank at 8 pm. On Tuesday, B alone completed filling the tank at 6 pm. On Wednesday, A alone worked till 5 pm, and then B worked alone from 5 pm to 7 pm, to fill the tank. At what time was the tank filled on Thursday if both pumps were used simultaneously all along?
Started 3 months ago by Shashank in
Explanatory Answer
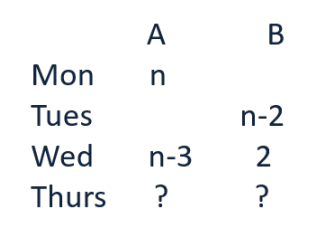
Given that a tank is emptied everyday at a fixed time point and after that either pump A or B or
both start working to fill the tank.
On Monday, A alone completed filling the tank at 8 pm.
On Tuesday, B alone completed filling the tank at 6 pm.
On Wednesday, A alone worked till 5 pm, and then B worked alone from 5 pm to 7 pm, to fill the
tank.
We have to find at what time will the tank filled on thursday if both were used simultaneously all
along
A is doing 3 hours less work on Wednesday which B completes in 2 hours therefore B = 1.5 A
⟹ (n)/(n-2) = 3/2
⟹ 2n = 3n – 6
⟹ n = 6
A takes 6 hours and B takes 4 hours or the tank is closed at 2 pm
When they are together open
⟹ 1/6 + 1/4 = (2+3)/12
⟹ Rate is 5/12 or they can fill the entire tank in 12/5 hours which is 2 hours 24 minutes
Starting from 2 pm, they fill the entire tank by 4:24 pm
Here the break through is figuring out the ratio or efficiency of the rate at which they fill is B : A
= 3 : 2
The conventional way is
⟹ (n−3)/n + 2/(n-2) = 1
n-3 hours at the rate of 1/𝑛 per hour
2 hours at the rate 1/(𝑛−2) per hour
Solving this we get n = 6 and we can find solution using this n.
-
No one is replied to this question yet. Be first to reply!
