A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is
Started 3 months ago by Shashank in
Explanatory Answer
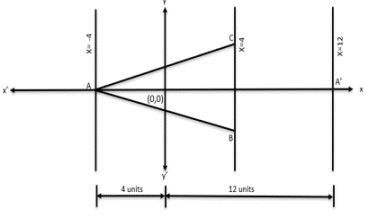
Given Area (△ABC) = 32 sq units and one of the length BC = 8 units on the line x = 4
Let us draw a graph and plot the given values.
We know that area of the Triangle = 1/2 × base × height considering BC as the base,
area of the Triangle = 1/2 × 8 × height = 32
Height = (32×2) / 8 = 64/8 = 8 units
Since the base lies on x = 4 and has a vertical height is of length = 8 units, A can either lie on the
line x = 12 or on x = - 4
However, since we need to find the shortest possible distance between A and the origin, A should
lie on the line x = - 4
So, shortest possible distance to A from the point (0,0) = 4 units
-
No one is replied to this question yet. Be first to reply!
