For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
Started 3 months ago by Shashank in
Explanatory Answer
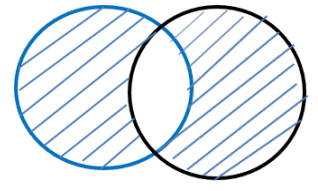
Given that for two sets A and B, A △ B denote the set of elements which belong to A or B but not
both.
This is the diagram which represents A △ B ,the set of elements which belongs to A or B i.e. A
intersection B subtracted from A union B
We have to find the number of elements in (P △ Q) △ (R △ S) if
P = {1 , 2 , 3 , 4} Q = {2 , 3 , 5 , 6 ,} R = {1 , 3 , 7 , 8 , 9} S = {2 , 4 , 9 , 10}
For P △ Q, we have to find the elements which do not to belong to both P and Q such that
(P △ Q) = {1, 4 , 5 , 6}
(R △ S) = {1 , 2 , 3 , 4 , 7 , 8 , 10}
(P △ Q) △ (R △ S) = {2 , 3 , 5 , 7 , 6 , 8 , 10}
The number of elements (P △ Q) △ (R △ S) is 7
-
No one is replied to this question yet. Be first to reply!
