Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is &nbsp;

CAT 2022 Question Paper | CAT Verbal Ability Slot 3

Question :

Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is

Started 1 week ago by Shashank in

0 11

Answer : The answer is '9'

Explanatory Answer

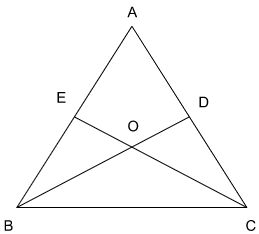
Triangle

O is the centroid of the triangle ABC,that means,
BO : OD = 2 : 1
CO : OE = 2 : 1
Ar(BOC) : Ar(ODC) = 2 : 1
Ar(COB) : Ar(OEB) = 2 : 1

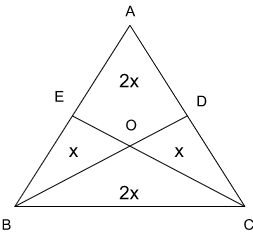
Triangle

Since BD is the median, Ar(BDA) = Ar(BDC)
This means Ar(AEOD) = 2x
2x + x + x + 2x = 108
6x = 108
Ar(AEOD) = 2x = 36

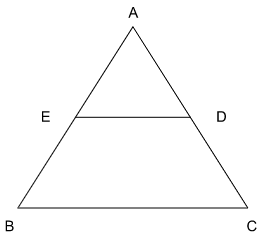
Triangle

Since ED is the line joining the midpoints of AB and AC, Ar(AED) = ¼ Ar(ABC)
Ar(AED) = ¼ Ar(108) = 27
Ar(EOD) = Ar(AEOD) - Ar(AED) = 36 - 27 = 9 sq cm