Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
419
Learners
asked the doubt
Previous Year Questions
Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
Video Explanation
Explanatory Answer
Since AOB is a right-angled triangle and AO = 4m, BO = 3m
AB = 5m
Dropping a perpendicular from O on AB at D, we know that:
OA * OB = AB * OD
4*3 = 5*OD
OD = 12/5
We know that OD bisects the chord PQ. Hence, PD = QD
Also, in triangle OPD:
OD 2 + PD 2 = OP 2
(12/5) 2 + PD 2 = 5 2 = 25
PD 2 = 25 – 144/25 = (625 – 144)/25 = 481/25
PD = Ö 481/5 ̴ 21.9/5 = 4.4
PQ = 2*PD = 8.8
Video Explanation
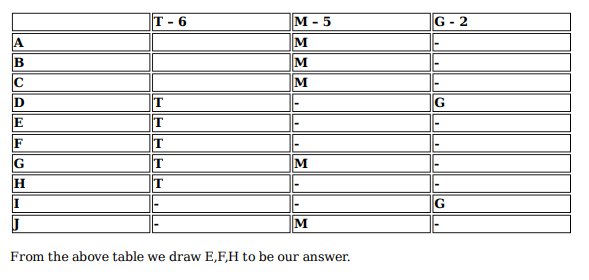
Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation
Explanatory Answer
Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation
Explanatory Answer
If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation
Explanatory Answer
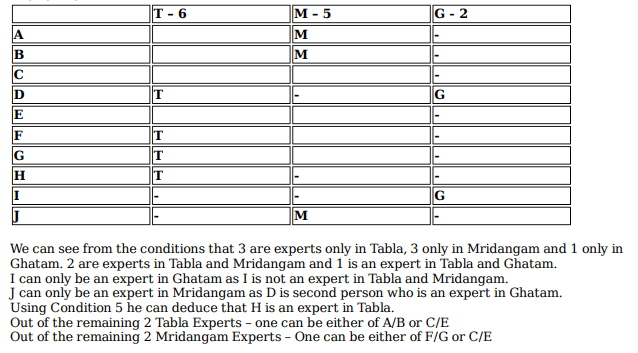
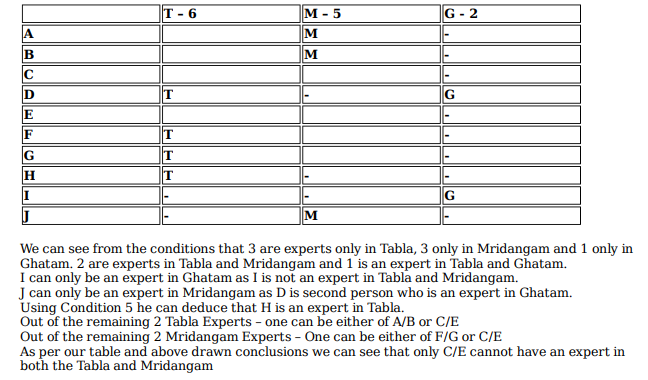
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation
Explanatory Answer
Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation
Explanatory Answer
Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation
Explanatory Answer
If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation
Explanatory Answer
Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation
Explanatory Answer
Video Explanation
Explanatory Answer
Video Explanation
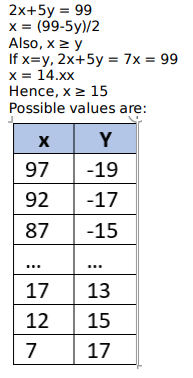
The number of pairs of integers(x,y) satisfying x ≥ y ≥ -20 and 2x + 5y = 99 is
Video Explanation
Explanatory Answer
From the interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the perpendiculars is 's'. Then the area of the triangle is
Video Explanation
Explanatory Answer
Let OP, OQ, and OR be 3 altitudes drawn from the centroid of the
equilateral triangle.
Length of all 3 p erpendicular s will be equal . Therefore, length of
OP = OQ = OR = s/3
AP is the altitude of the triangle. We know that the centroid divides
the altitude in the ratio 2:1
Hence, AO : OP = 2:1
AO = 2s/3
AP = AO + OP = s
Let side of triangle be ‘a’
Altitude AP = s = Ö 3a/2
a = 2s/ Ö 3
Area of triangle = (½)*a*s
= (½)*2s/ Ö 3*s
= s 2 / Ö 3
In a car race, car A beats car B by 45 km, car B beats car C by 50 km, and car A beats car C by 90 km. The distance (in km) over which the race has been conducted is
Video Explanation
Who all are NOT guiding any Economics students?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
R & T are guiding Economics students while P, Q, and S are not.
Which of the following statements is necessarily true?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
• S may be guiding either of ‘F’ or ‘G’, so not necessarily true
• Similarly, Q may be guiding either of ‘F’ or ‘G’, so not necessarily true
• We are sure that ‘H’ is an Economics student, hence TRUE
• ‘B’ is scheduled in the second slot, hence False
If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation
Explanatory Answer
• If ‘D’ is scheduled in a slot later than Q’s, it means that Q must be in the 9.30am slot, guiding ‘G’.
Hence, S is in the 10.30am slot guiding ‘F’.
• Also, it implies that ‘D’ must be scheduled in the 10.30 slot guided by R, and ‘E’ & ‘H’ are in the
9am or 9.30am slot guided by T.
Hence, both statements are true.
If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation
Explanatory Answer
• If Q is scheduled in the 9.30am slot guiding ‘G’, ‘E’ must also be in 9.30am slot guided by T.
• If Q is scheduled in the 10.30am slot guiding ‘F’, ‘E’ must also be in 10.30am slot guided by R.
Hence, no new inferences can be gained from this information.
Since ‘A’ is guided by R, at least one of ‘D’ and ‘H’ will have to be guided by T.
If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation
Explanatory Answer
If Q is in 10.30am slot, ‘D’ must be in 10am slot. But that is not feasible as A is in the 10am slot
already and no 2 Eco students are in the same slot.
Hence, Q must be in the 9.30am slot and ‘D’ in the 9am slot guided by T. We can see from the
solution that ‘E’ may be guided by either R or T.
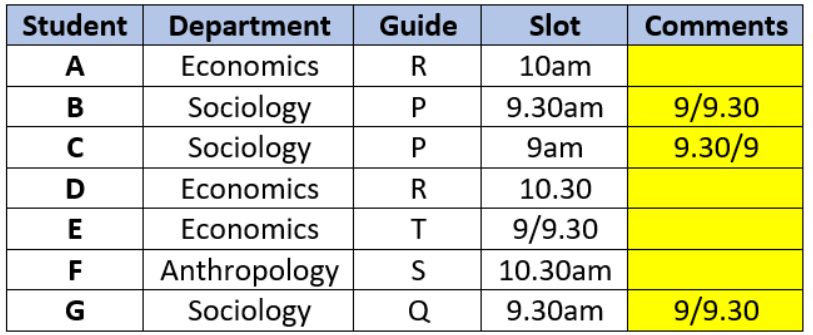
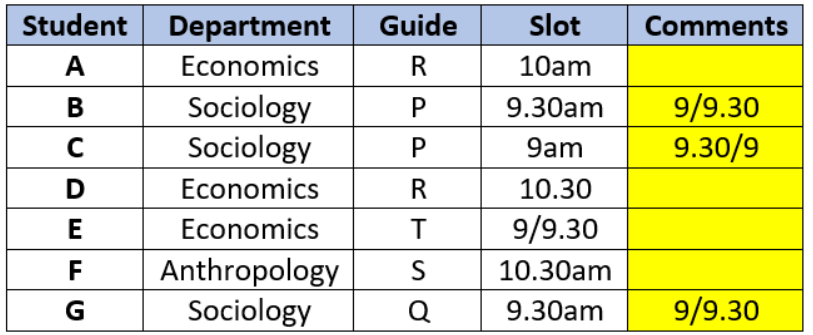
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Which one of the following statements is true?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
A is clear from the solution, the first slot has 2 seminars.
Who all are NOT guiding any Economics students?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
R & T are guiding Economics students while P, Q, and S are not.
Which of the following statements is necessarily true?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
• S may be guiding either of ‘F’ or ‘G’, so not necessarily true
• Similarly, Q may be guiding either of ‘F’ or ‘G’, so not necessarily true
• We are sure that ‘H’ is an Economics student, hence TRUE
• ‘B’ is scheduled in the second slot, hence False
If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation
Explanatory Answer
• If ‘D’ is scheduled in a slot later than Q’s, it means that Q must be in the 9.30am slot, guiding ‘G’.
Hence, S is in the 10.30am slot guiding ‘F’.
• Also, it implies that ‘D’ must be scheduled in the 10.30 slot guided by R, and ‘E’ & ‘H’ are in the
9am or 9.30am slot guided by T.
Hence, both statements are true.
If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation
Explanatory Answer
• If Q is scheduled in the 9.30am slot guiding ‘G’, ‘E’ must also be in 9.30am slot guided by T.
• If Q is scheduled in the 10.30am slot guiding ‘F’, ‘E’ must also be in 10.30am slot guided by R.
Hence, no new inferences can be gained from this information.
Since ‘A’ is guided by R, at least one of ‘D’ and ‘H’ will have to be guided by T.
If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation
Explanatory Answer
If Q is in 10.30am slot, ‘D’ must be in 10am slot. But that is not feasible as A is in the 10am slot
already and no 2 Eco students are in the same slot.
Hence, Q must be in the 9.30am slot and ‘D’ in the 9am slot guided by T. We can see from the
solution that ‘E’ may be guided by either R or T.
Which one of the following statements is true?
Video Explanation
Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
A is clear from the solution, the first slot has 2 seminars.
The number of patients who were treated with medicine type D was:
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
a. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine type B?
Video Explanation
Explanatory Answer
Using the Question we are able to fill the Venn diagram in the following manner.
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
How many patients were treated with medicine types B and D only?
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
The number of patients who were treated with medicine type D was:
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
How many patients were treated with medicine type B?
Video Explanation
Explanatory Answer
Using the Question we are able to fill the Venn diagram in the following manner.
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
How many patients were treated with medicine types B and D only?
Video Explanation
Explanatory Answer
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?
Video Explanation
Explanatory Answer
Total number of valid votes in 4 constituencies = 5,00,000 + 3,25,000 + 6,00,030 + 1,75,000
= 16,00,030
We can consolidate the data about the candidates who lost security in the below table:
Therefore, total number of votes polled by candidates who lost their security deposit:
45,000 + 2,76,250 + 0 + 61,250 = 3,82,500
% = (3,82,500/16,00, 030)* 100 = 23.9%
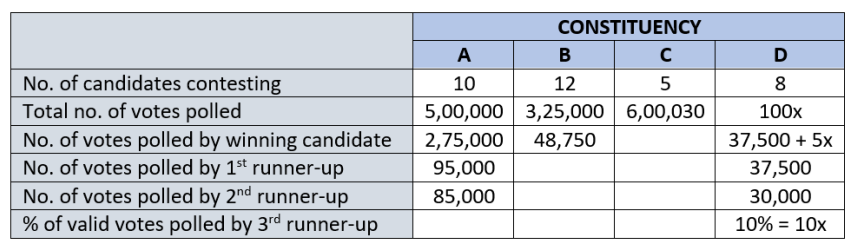
In an election several candidates contested for a constituency. In any constituency, the winning candidate was the one who polled the highest number of votes, the first runner up was the one who polled the second highest number of votes, the second runner up was the one who polled the third highest number of votes, and so on. There were no ties (in terms of number of votes polled by the candidates) in any of the constituencies in this election.
In an electoral system, a security deposit is the sum of money that a candidate is required to pay to the election commission before he or she is permitted to contest. Only the defeated candidates (i.e., one who is not the winning candidate) who fail to secure more than one sixth of the valid votes polled in the constituency, lose their security deposits.
The following table provides some incomplete information about votes polled in four constituencies: A, B, C and D, in this election.
The following additional facts are known:
1. The first runner up polled 10,000 more votes than the second runner up in constituency A. 2. None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000.
3. The winning candidate in constituency D polled 5% of valid votes more than that of the first runner up. All the candidates who lost their security deposits while contesting for this constituency, put together, polled 35% of the valid votes.
What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in A = 5,00,000
Total votes polled by top 3 candidates = 2,75,000 + 95,000 + 85,000 = 4,55,000
Votes polled by bottom 7 candidates = 5,00,000 – 4,55,000 = 45,000
We can see that 45,000 is clearly less than 1/6 th of 5,00,000 (83,333) . Hence, all the bottom 7
candidates lost their deposit.
Total % votes polled by them = \(({45000 \over {500000}})*100\) = 9%
How many candidates who contested in constituency B lost their security deposit?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in B = 3,25,000
1/6 th of 325000 = 54166.66 ̴ 54167
We can see that the winning candidate also secured less than 1/6 th of the total valid votes.
Hence, the rest 11 candidates must have secured lesser votes than that.
Hence, 11 candidates lost their security deposit in B.
What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total no. of votes polled in C = 6,00,030
Total no. of candidates = 5
We know that everyone polled more than 1,00,005 votes in C, and minimum diff between any 2 is
10,000.
Hence, minimum votes polled by bottom 4 :
( 1,00,006 ) + ( 1,00, 006 + 10 000) + (1,00,006 + 2*10000) + (1,00,006 + 3*10000)
= 4*1,00,006 + 60,000 = 4,60,024 votes
Maximum votes polled by winning candidate = 6,00,030 – 4,60,024 = 1,40,006
Minimum votes polled by 1 st runner-up = 1,00,006 + 30,000 = 1,30,006
Diff between the two is 10,000. Hence, we can conclude that winner polled exactly 1,40,006
votes.
What was the number of valid votes polled in constituency D?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in D = 100x
Votes secured by top 4 = 37,500 + 5x + 37,500 + 30,000 + 10x = 1,05,000 + 15x
We can also see that the 3 rd runner-up secured less than 1/6 th (10%) votes and hence lost
security deposit. So, minimum 5 and maximum 7 candidates lost security deposit.
We can have 3 cases here:
CASE I: 7 candidates (all except winner) lost security deposit. In this case, top candidate will
have remining 65% votes.
37,500 + 5x = 65x
60x = 37,500
x = 625
Total votes polled = 100x = 62 , 500
1/6 th of 62,500 = 10,417
Votes secured by 1 st runner-up = 37,500 > 10,417
1 st runner up couldn’t have lost deposit. Hence, this case is not feasible.
CASE II: 6 candidates (all except winner & 1 st runner-up) lost security deposit. In this case, top 2
candidates will have remining 65% votes.
37,500 + 5x + 37,500 = 65x
75,000 = 60x
x = 1250
Total votes polled = 100x = 1,25,000
1/6 th of 1,25,000 = 20,833
Once again, 1 st runner-up secured more than 1/6 th votes and couldn’t have lost deposit. This
case is also not feasible.
CASE III: 5 candidates (all except winner, 1 st runner-up & 2 nd runner-up) lost security deposit.
In this case, top 3 candidates will have remining 65% votes.
75,000 + 5x + 30,000 = 65x
60x = 1,05,000
x = 17 50
Total votes polled = 100x = 1,75,000
1/6 th of 1,75,000 = 29,167
Votes secured by 3 rd runner-up = 10x = 10,500 < 29,167
Hence, this is the only feasible case.
Therefore, total number of valid votes polled in D is 1,75,000.
The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?
Video Explanation
Explanatory Answer
The confirmed order we know is D < C < A. ‘B’ could be anywhere in between except more than
A.
Hence, B < C < D < A is not possible as we know that margin of C is greater than that of D.
For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?
Video Explanation
Explanatory Answer
Total number of valid votes in 4 constituencies = 5,00,000 + 3,25,000 + 6,00,030 + 1,75,000
= 16,00,030
We can consolidate the data about the candidates who lost security in the below table:
Therefore, total number of votes polled by candidates who lost their security deposit:
45,000 + 2,76,250 + 0 + 61,250 = 3,82,500
% = (3,82,500/16,00, 030)* 100 = 23.9%
What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in A = 5,00,000
Total votes polled by top 3 candidates = 2,75,000 + 95,000 + 85,000 = 4,55,000
Votes polled by bottom 7 candidates = 5,00,000 – 4,55,000 = 45,000
We can see that 45,000 is clearly less than 1/6 th of 5,00,000 (83,333) . Hence, all the bottom 7
candidates lost their deposit.
Total % votes polled by them = \(({45000 \over {500000}})*100\) = 9%
How many candidates who contested in constituency B lost their security deposit?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in B = 3,25,000
1/6 th of 325000 = 54166.66 ̴ 54167
We can see that the winning candidate also secured less than 1/6 th of the total valid votes.
Hence, the rest 11 candidates must have secured lesser votes than that.
Hence, 11 candidates lost their security deposit in B.
What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total no. of votes polled in C = 6,00,030
Total no. of candidates = 5
We know that everyone polled more than 1,00,005 votes in C, and minimum diff between any 2 is
10,000.
Hence, minimum votes polled by bottom 4 :
( 1,00,006 ) + ( 1,00, 006 + 10 000) + (1,00,006 + 2*10000) + (1,00,006 + 3*10000)
= 4*1,00,006 + 60,000 = 4,60,024 votes
Maximum votes polled by winning candidate = 6,00,030 – 4,60,024 = 1,40,006
Minimum votes polled by 1 st runner-up = 1,00,006 + 30,000 = 1,30,006
Diff between the two is 10,000. Hence, we can conclude that winner polled exactly 1,40,006
votes.
What was the number of valid votes polled in constituency D?
Video Explanation
Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
Total votes polled in D = 100x
Votes secured by top 4 = 37,500 + 5x + 37,500 + 30,000 + 10x = 1,05,000 + 15x
We can also see that the 3 rd runner-up secured less than 1/6 th (10%) votes and hence lost
security deposit. So, minimum 5 and maximum 7 candidates lost security deposit.
We can have 3 cases here:
CASE I: 7 candidates (all except winner) lost security deposit. In this case, top candidate will
have remining 65% votes.
37,500 + 5x = 65x
60x = 37,500
x = 625
Total votes polled = 100x = 62 , 500
1/6 th of 62,500 = 10,417
Votes secured by 1 st runner-up = 37,500 > 10,417
1 st runner up couldn’t have lost deposit. Hence, this case is not feasible.
CASE II: 6 candidates (all except winner & 1 st runner-up) lost security deposit. In this case, top 2
candidates will have remining 65% votes.
37,500 + 5x + 37,500 = 65x
75,000 = 60x
x = 1250
Total votes polled = 100x = 1,25,000
1/6 th of 1,25,000 = 20,833
Once again, 1 st runner-up secured more than 1/6 th votes and couldn’t have lost deposit. This
case is also not feasible.
CASE III: 5 candidates (all except winner, 1 st runner-up & 2 nd runner-up) lost security deposit.
In this case, top 3 candidates will have remining 65% votes.
75,000 + 5x + 30,000 = 65x
60x = 1,05,000
x = 17 50
Total votes polled = 100x = 1,75,000
1/6 th of 1,75,000 = 29,167
Votes secured by 3 rd runner-up = 10x = 10,500 < 29,167
Hence, this is the only feasible case.
Therefore, total number of valid votes polled in D is 1,75,000.
The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?
Video Explanation
Explanatory Answer
The confirmed order we know is D < C < A. ‘B’ could be anywhere in between except more than
A.
Hence, B < C < D < A is not possible as we know that margin of C is greater than that of D.
What was the increase in sales amount, in Crore Rupees, in the Apparel department of Mumbai from 2018 to 2019?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
Mumbai’s sales in Apparel department increased by 12 crores (62cr – 50cr)
Among all the 12 departments (i.e., the 3 departments in each of the 4 cities), what was the maximum percentage increase in sales amount from 2018 to 2019?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
We see maximum percentage increase in the Home Décor department in Mumbai, increasing from
48 to 72.
Increase = [(72-48)/ 48]* 100 = 50%
What was the total sales amount, in Crore Rupees, in 2019 for the chain of departmental stores?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
Total sales amount in 2019:
(50 + 62 + 58 + 54) + (98 + 102 + 70 + 100) + (100 + 72 + 80 + 54)
= (224) + (370) + (306)
= 900 crores
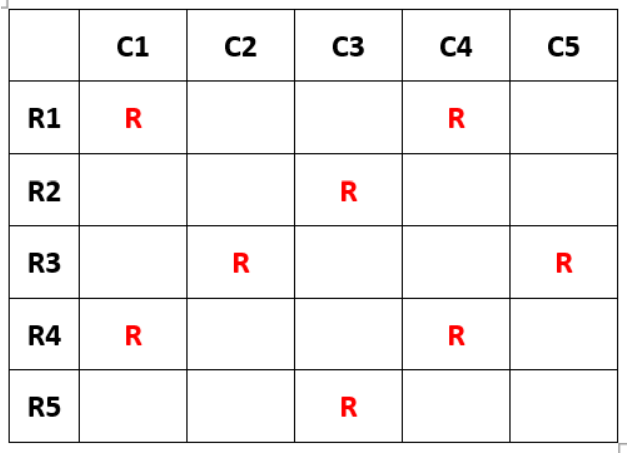
A chain of departmental stores has outlets in Delhi, Mumbai, Bengaluru and Kolkata. The sales are categorized by its three departments – ‘Apparel’, ‘Electronics’, and ‘HomeDecor’. An Accountant has been asked to prepare a summary of the 2018 and 2019 sales amounts for an internal report. He has collated partial information and prepared the following table.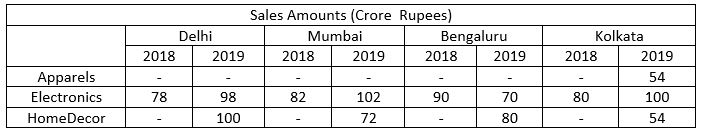
The following additional information is known.
1. The sales amounts in the Apparel departments were the same for Delhi and Kolkata in 2018.
2. The sales amounts in the Apparel departments were the same for Mumbai and Bengaluru in 2018. This sales amount matched the sales amount in the Apparel department for Delhi in 2019.
3. The sales amounts in the HomeDecor departments were the same for Mumbai and Kolkata in 2018.
4. The sum of the sales amounts of four Electronics departments increased by the same amount as the sum of the sales amounts of four Apparel departments from 2018 to 2019.
5. The total sales amounts of the four HomeDecor departments increased by Rs 70 Crores from 2018 to 2019.
6. The sales amounts in the HomeDecor departments of Delhi and Bengaluru each increased by Rs 20 Crores from 2018 to 2019.
7. The sales amounts in the Apparel departments of Delhi and Bengaluru each increased by the same amount in 2019 from 2018. The sales amounts in the Apparel departments of Mumbai and Kolkata also each increased by the same amount in 2019 from 2018.
8. The sales amounts in the Apparel departments of Delhi, Kolkata and Bengaluru in 2019 followed an Arithmetic Progression.
In HomeDecor departments of which cities were the sales amounts the highest in 2018 and 2019, respectively?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
We can see form the table that Delhi had the highest sales amount in Home Décor in both the
years.
What was the increase in sales amount, in Crore Rupees, in the Apparel department of Mumbai from 2018 to 2019?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
Mumbai’s sales in Apparel department increased by 12 crores (62cr – 50cr)
Among all the 12 departments (i.e., the 3 departments in each of the 4 cities), what was the maximum percentage increase in sales amount from 2018 to 2019?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
We see maximum percentage increase in the Home Décor department in Mumbai, increasing from
48 to 72.
Increase = [(72-48)/ 48]* 100 = 50%
What was the total sales amount, in Crore Rupees, in 2019 for the chain of departmental stores?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
Total sales amount in 2019:
(50 + 62 + 58 + 54) + (98 + 102 + 70 + 100) + (100 + 72 + 80 + 54)
= (224) + (370) + (306)
= 900 crores
In HomeDecor departments of which cities were the sales amounts the highest in 2018 and 2019, respectively?
Video Explanation
Explanatory Answer
From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:
We can see form the table that Delhi had the highest sales amount in Home Décor in both the
years.
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1, 3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Initially cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?
Video Explanation
Explanatory Answer
Hence, cars 7 & 2 are parked near car 3.
Suppose eight cars have arrived, of which two have left. Also suppose that car 4 is a compact and car 7 is an SUV. Which of the following is a POSSIBLE current configuration of the parking lot?
Video Explanation
Explanatory Answer
From the options, we can understand that initially, cars 1-6 were in the lot, post which 1 & 4 left
and 7 & 8 came in.
Suppose the sequence at some point of time is 4, 5, 6, V, 3. Which of the following is NOT necessarily true?
Video Explanation
Suppose that car 4 is not the first car to leave and that the sequence at a time between the arrival of the car 7 and car 8 is V, 7, 3, 6, 5. Then which of the following statements MUST be false?
Video Explanation
Initially cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?
Video Explanation
Explanatory Answer
Hence, cars 7 & 2 are parked near car 3.
Suppose eight cars have arrived, of which two have left. Also suppose that car 4 is a compact and car 7 is an SUV. Which of the following is a POSSIBLE current configuration of the parking lot?
Video Explanation
Explanatory Answer
From the options, we can understand that initially, cars 1-6 were in the lot, post which 1 & 4 left
and 7 & 8 came in.
Suppose the sequence at some point of time is 4, 5, 6, V, 3. Which of the following is NOT necessarily true?
Video Explanation
Suppose that car 4 is not the first car to leave and that the sequence at a time between the arrival of the car 7 and car 8 is V, 7, 3, 6, 5. Then which of the following statements MUST be false?
Video Explanation
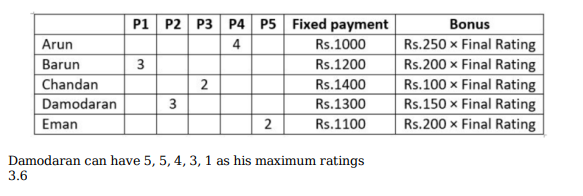
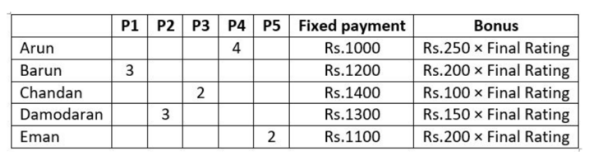
The local office of the APP-CAB company evaluates the performance of five cab drivers, Arun,
Barun, Chandan, Damodaran, and Eman for their monthly payment based on ratings in five
different parameters (P1 to P5) as given below:
P1: timely arrival
P2: behaviour
P3: comfortable ride
P4: driver's familiarity with the route
P5: value for money
Based on feedback from the customers, the office assigns a rating from 1 to 5 in each of these
parameters. Each rating is an integer from a low value of 1 to a high value of 5. The final rating
of a driver is the average of his ratings in these five parameters. The monthly payment of the
drivers has two parts – a fixed payment and final rating-based bonus. If a driver gets a rating of 1
in any of the parameters, he is not eligible to get bonus. To be eligible for bonus a driver also
needs to get a rating of five in at least one of the parameters.
The partial information related to the ratings of the drivers in different parameters and the
monthly payment structure (in rupees) is given in the table below:
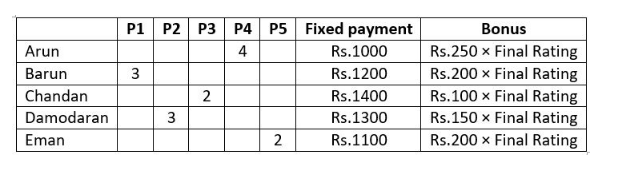
The following additional facts are known.
1. Arun and Barun have got a rating of 5 in exactly one of the parameters. Chandan has got a
rating of 5 in exactly two parameters.
2. None of drivers has got the same rating in three parameters.
If Damodaran does not get a bonus, what is the maximum possible value of his final rating?
Video Explanation
Explanatory Answer
If Eman gets a bonus, what is the minimum possible value of his final rating?
Video Explanation
Explanatory Answer
If all five drivers get bonus, what is the minimum possible value of the monthly payment (in rupees) that a driver gets?
Video Explanation
Explanatory Answer
If all five drivers get bonus, what is the maximum possible value of the monthly payment (in rupees) that a driver gets?
Video Explanation
Explanatory Answer
If Damodaran does not get a bonus, what is the maximum possible value of his final rating?
Video Explanation
Explanatory Answer
If Eman gets a bonus, what is the minimum possible value of his final rating?
Video Explanation
Explanatory Answer
If all five drivers get bonus, what is the minimum possible value of the monthly payment (in rupees) that a driver gets?
Video Explanation
Explanatory Answer
If all five drivers get bonus, what is the maximum possible value of the monthly payment (in rupees) that a driver gets?
Video Explanation
Explanatory Answer
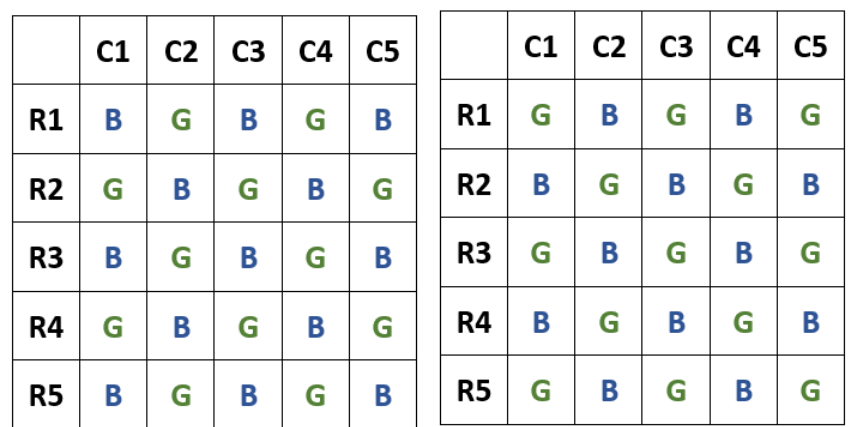
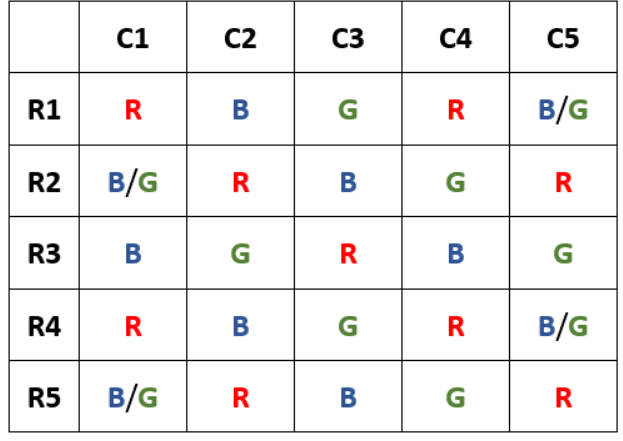
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Every unique, complete arrangement of twenty five beads is called a configuration.
The total number of possible congurations using beads of only two colours is:
Video Explanation
Explanatory Answer
Rules:
• Adjacent beads of different colours
• At least one green bead between any 2 blue beads
• At least one green & at least one blue bead between any 2 red beads
It is clear that using Red would require the other 2 colours too. Hence, combinations of Red +
Blue and Red + Green are not possible.
Using Blue + Green combination:
2 arrangements are possible
What is the maximum possible number of Red beads that can appear in any conguration?
Video Explanation
Explanatory Answer
Maximum number of Red beads possible in a configuration = 9
What is the minimum number of Blue beads in any conguration?
Video Explanation
Explanatory Answer
Minimum number of Blue beads possible in a configuration = 6
Two Red beads have been placed in ‘second row, third column’ and ‘third row, second column’. How many more Red beads can be placed so as to maximise the number of Red beads used in the configuration?
Video Explanation
Explanatory Answer
If we place 2 red beads at R2-C3 and R3-C2, the rest of the red beads can be maximised in the
following way:
A total of 8 red beads can be placed in this configuration. Hence, we can place 6 more red
beads to maximise their number.
The total number of possible congurations using beads of only two colours is:
Video Explanation
Explanatory Answer
Rules:
• Adjacent beads of different colours
• At least one green bead between any 2 blue beads
• At least one green & at least one blue bead between any 2 red beads
It is clear that using Red would require the other 2 colours too. Hence, combinations of Red +
Blue and Red + Green are not possible.
Using Blue + Green combination:
2 arrangements are possible
