Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
419
Learners
asked the doubt
Previous Year Questions
The author critiques meritocracy for all the following reasons EXCEPT that:
Video Explanation
Explanatory Answer
The complexity of modern problems often precludes any one person from fully understanding them. Factors contributing to rising obesity levels, for example, include transportation systems and infrastructure, media, convenience foods, changing social norms, human biology and psychological factors. The multidimensional or layered character of complex problems also undermines the principle of meritocracy: the idea that the ‘best person’ should be hired. There is no best person. When putting together an oncological research team, a biotech company such as Gilead or Genentech would not construct a multiple-choice test and hire the top scorers, or hire people whose resumes score highest according to some performance criteria. Instead, they would seek diversity. They would build a team of people who bring diverse knowledge bases, tools and analytic skills.
Believers in a meritocracy might grant that teams ought to be diverse but then argue that meritocratic principles should apply within each category. Thus the team should consist of the ‘best’ mathematicians, the ‘best’ oncologists, and the ‘best’ biostatisticians from within the pool. That position suffers from a similar flaw.
Even with a knowledge domain, no test or criteria applied to individuals will produce the best team. Each of these domains possesses such depth and breadth, that no test can exist. Consider the field of neuroscience. Upwards of 50,000 papers were published last year covering various techniques, domains of enquiry and levels of analysis, ranging from molecules and synapses up through networks of neurons. Given that complexity, any attempt to rank a collection of neuroscientists from best to worst, as if they were competitors in the 50-metre butterfly, must fail. What could be true is that given a specific task and the composition of a particular team, one scientist would be more likely to contribute than another. Optimal hiring depends on context. Optimal teams will be diverse.
Evidence for this claim can be seen in the way that papers and patents that combine diverse ideas tend to rank as high-impact. It can also be found in the structure of the so-called random decision forest, a state-of-the-art machine-learning algorithm.
Random forests consist of ensembles of decision trees. If classifying pictures, each tree makes a vote: is that a picture of a fox or a dog? A weighted majority rules. Random forests can serve many ends. They can identify bank fraud and diseases, recommend ceiling fans and predict online dating behaviour. When building a forest, you do not select the best trees as they tend to make similar classifications. You want diversity. Programmers achieve that diversity by training each tree on different data, a technique known as bagging. They also boost the forest ‘cognitively’ by training trees on the hardest cases – those that the current forest gets wrong. This ensures even more diversity and accurate forests."
Yet the fallacy of meritocracy persists. Corporations, non-profits, governments, universities and even preschools test, score and hire the ‘best’. This all but guarantees not creating the best team. Ranking people by common criteria produces homogeneity. That’s not likely to lead to breakthroughs.
The author critiques meritocracy for all the following reasons EXCEPT that:
Video Explanation
Explanatory Answer
Which of the following conditions would weaken the efficacy of a random decision forest?
Video Explanation
Explanatory Answer
Which of the following conditions, if true, would invalidate the passage’s main argument?
Video Explanation
Explanatory Answer
On the basis of the passage, which of the following teams is likely to be most effective in solving the problem of rising obesity levels?
Video Explanation
Explanatory Answer
Which of the following best describes the purpose of the example of neuroscience?
Video Explanation
Explanatory Answer
All of the following evidence supports the passage’s explanation of sea travel/trade EXCEPT:
Video Explanation
Explanatory Answer
Grove snails as a whole are distributed all over Europe, but a specific variety of the snail, with a distinctive white-lipped shell, is found exclusively in Ireland and in the Pyrenees mountains that lie on the border between France and Spain. The researchers sampled a total of 423 snail specimens from 36 sites distributed across Europe, with an emphasis on gathering large numbers of the white-lipped variety. When they sequenced genes from the mitochondrial DNA of each of these snails and used algorithms to analyze the genetic diversity between them, they found that a distinct lineage (the snails with the white-lipped shells) was indeed endemic to the two very specific and distant places in question.
Explaining this is tricky. Previously, some had speculated that the strange distributions of creatures such as the white-lipped grove snails could be explained by convergent evolution—in which two populations evolve the same trait by coincidence—but the underlying genetic similarities between the two groups rules that out. Alternately, some scientists had suggested that the white-lipped variety had simply spread over the whole continent, then been wiped out everywhere besides Ireland and the Pyrenees, but the researchers say their sampling and subsequent DNA analysis eliminate that possibility too.
“If the snails naturally colonized Ireland, you would expect to find some of the same genetic type in other areas of Europe, especially Britain. We just don’t find them,” Davidson, the lead author, said in a press statement.
Moreover, if they’d gradually spread across the continent, there would be some genetic variation within the white-lipped type, because evolution would introduce variety over the thousands of years it would have taken them to spread from the Pyrenees to Ireland. That variation doesn’t exist, at least in the genes sampled. This means that rather than the organism gradually expanding its range, large populations instead were somehow moved en mass to the other location within the space of a few dozen generations, ensuring a lack of genetic variety.
“There is a very clear pattern, which is difficult to explain except by involving humans,” Davidson said. Humans, after all, colonized Ireland roughly 9,000 years ago, and the oldest fossil evidence of grove snails in Ireland dates to roughly the same era. Additionally, there is archaeological evidence of early sea trade between the ancient peoples of Spain and Ireland via the Atlantic and even evidence that humans routinely ate these types of snails before the advent of agriculture, as their burnt shells have been found in Stone Age trash heaps.
The simplest explanation, then? Boats. These snails may have inadvertently traveled on the floor of the small, coast-hugging skiffs these early humans used for travel, or they may have been intentionally carried to Ireland by the seafarers as a food source. “The highways of the past were rivers and the ocean–as the river that flanks the Pyrenees was an ancient trade route to the Atlantic, what we’re actually seeing might be the long lasting legacy of snails that hitched a ride as humans travelled from the South of France to Ireland 8,000 years ago,” Davidson said.
All of the following evidence supports the passage’s explanation of sea travel/trade EXCEPT:
Video Explanation
Explanatory Answer
The passage outlines several hypotheses and evidence related to white-lipped grove snails to arrive at the most convincing explanation for:
Video Explanation
Explanatory Answer
Which one of the following makes the author eliminate convergent evolution as a probable explanation for why white-lipped grove snails are found in Ireland and the Pyrenees?
Video Explanation
Explanatory Answer
In paragraph 4, the evidence that “humans routinely ate these types of snails before the advent of agriculture” can be used to conclude that:
Video Explanation
Explanatory Answer
The passage outlines several hypotheses and evidence related to white-lipped grove snails to arrive at the most convincing explanation for:
Video Explanation
Explanatory Answer
Which one of the following makes the author eliminate convergent evolution as a probable explanation for why white-lipped grove snails are found in Ireland and the Pyrenees?
Video Explanation
Explanatory Answer
In paragraph 4, the evidence that “humans routinely ate these types of snails before the advent of agriculture” can be used to conclude that:
Video Explanation
Explanatory Answer
What was the buying exchange rate of currency C with respect to currency L on that day?
Video Explanation
What was the base exchange rate of currency B with respect to currency L on that day? [TITA]
Video Explanation
How many units of currency C did the outlet sell on that day?
Video Explanation
How many units of currency A did the outlet buy on that day? [TITA]
Video Explanation
Currency Exchange
The base exchange rate of a currency X with respect to a currency Y is the number of units of currency Y which is equivalent in value to one unit of currency X. Currency exchange outlets buy currency at buying exchange rates that are lower than base exchange rates, and sell currency at selling exchange rates that are higher than base exchange rates.
A currency exchange outlet uses the local currency L to buy and sell three international currencies A, B, and C, but does not exchange one international currency directly with another. The base exchange rates of A, B and C with respect to L are in the ratio 100:120:1. The buying exchange rates of each of A, B, and C with respect to L are 5% below the corresponding base exchange rates, and their selling exchange rates are 10% above their corresponding base exchange rates.
The following facts are known about the outlet on a particular day:
1. The amount of L used by the outlet to buy C equals the amount of L it received by selling C.
2. The amounts of L used by the outlet to buy A and B are in the ratio 5:3.
3. The amounts of L the outlet received from the sales of A and B are in the ratio 5:9.
4. The outlet received 88000 units of L by selling A during the day.
5. The outlet started the day with some amount of L, 2500 units of A, 4800 units of B, and 48000 units of C.
6. The outlet ended the day with some amount of L, 3300 units of A, 4800 units of B,and 51000 units of C.
How many units of currency A did the outlet buy on that day? [TITA]
Video Explanation
How many units of currency C did the outlet sell on that day?
Video Explanation
What was the base exchange rate of currency B with respect to currency L on that day? [TITA]
Video Explanation
What was the buying exchange rate of currency C with respect to currency L on that day?
Video Explanation
For how many digits can the complete list of letters associated with that digit be identified?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From
the above inferences, we can see that only two letters can be associated with digits for sure.
Which set of letters CANNOT be coded with the same digit?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
Consider option A S , U, V. We know that S takes 5. If both U and V takes 5 then there will be 4
letters coded to 5.
This is not possible.
What best can be concluded about the code for the letter B?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From the above inferences, we can see that B takes either 3 or 4.
What best can be concluded about the code for the letter L?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From the above inferences, we can see that L takes 1.
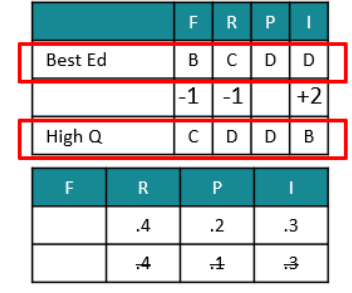
Letter Codes
According to a coding scheme the sentence,
Peacock is designated as the national bird of India is coded as 5688999 35 1135556678 56 458 13666689 1334 79 13366
This coding scheme has the following rules:
1. The scheme is case-insensitive (does not distinguish between upper case and lower case letters).
2. Each letter has a unique code which is a single digit from among 1,2,3,......,9.
3. The digit 9 codes two letters, and every other digit codes three letters.
4. The code for a word is constructed by arranging the digits corresponding to its letters in a non-decreasing sequence.
Answer these questions on the basis of this information
What best can be concluded about the code for the letter L?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From the above inferences, we can see that L takes 1.
What best can be concluded about the code for the letter B?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From the above inferences, we can see that B takes either 3 or 4.
For how many digits can the complete list of letters associated with that digit be identified?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
From
the above inferences, we can see that only two letters can be associated with digits for sure.
Which set of letters CANNOT be coded with the same digit?
Video Explanation
Explanatory Answer
Digits 1 to 8 are mapped to 3 letters each, 9 is mapped to only 2.
(3 × 8) + 2 = 26 which is the total number of letters in English.
Each letter is mapped to a unique code, but remember that each number is mapped
to 2323 letters.
It is best to start from the small words. Let us attack ‘is’ and ‘as’ first.
IS = 35, AS = 56. S = 5 , I = 3 , A = 6.
Now, THE is 458. OF = 79. PEACOCK does not have a ‘7’ in in. It has an O but no F, so F should be
7 and O should be 9.
THE has 458, DESIGNATED has T and E but no H. Is there a number in THE but not in
DESIGNATED?
H should be 4. T and E should be 5 and 8 in some order.
Now let us look at INDIA. INDIA = 13366. I = 3 and A = 6. So, N and D should be 1 and 6 in some
order. BIRD has a D, BIRD = 1334.
What does this mean? This tells us D = 1 and N = 6.
Let us have another look at T and E. T and E and 5 and 8 in some order. Is there a word that has
only one of T & E but not both?
NATIONAL has T but not E. NATIONAL has 8 but not 5. BINGO! We know T has to be 8 and E has
to be 5.
Now let us go word by word. PEACOCK = P56C9CK. So, PCCK should be 8899. 9 is allotted only
to two numbers.
We know that O = 9. So, what can we say about 9?
If C takes 8, then both P and K becomes 9 which is not possible as 9 can be assigned to only two
letters.
Therefore C has to take 9 and P , K takes the value 8.
DESIGNATED = 1553G66851. The missing number should be G. Or, G = 7.
NATIONAL = 6683966L. The missing number should be L. Or, L should be 1.
BIRD = B3R1. 3 and 4 are missing. B and R should be 3 and 4 in some order.
B and R occur only once each in this sequence, so there is no way of resolving this.
Consider option A S , U, V. We know that S takes 5. If both U and V takes 5 then there will be 4
letters coded to 5.
This is not possible.
The main purpose of the passage is to:
Video Explanation
Explanatory Answer
The author questions the use of monitoring systems in services that involve face-to-face interaction between service providers and clients because such systems:
Video Explanation
Explanatory Answer
Which of the following, IF TRUE, would undermine the passage’s main argument?
Video Explanation
Explanatory Answer
According to the author, service delivery in Indian education can be improved in all of the following ways EXCEPT through:
Video Explanation
Explanatory Answer
In the context of the passage, we can infer that the title “Band Aids on a Corpse” (in paragraph 2) suggests that:
Video Explanation
Explanatory Answer
Will a day come when India’s poor can access government services as easily as drawing cash from an ATM? No country in the world has made accessing education or health or policing or dispute resolution as easy as an ATM, because the nature of these activities requires individuals to use their discretion in a positive way. Technology can certainly facilitate this in a variety of ways if it is seen as one part of an overall approach, but the evidence so far in education, for instance, is that just adding computers alone doesn’t make education any better.
The dangerous illusion of technology is that it can create stronger, top down accountability of service providers in implementation-intensive services within existing public sector organisations. One notion is that electronic management information systems (EMIS) keep better track of inputs and those aspects of personnel that are ‘EMIS visible’ can lead to better services. A recent study examined attempts to increase attendance of Auxiliary Nurse Midwife (ANMs) at clinics in Rajasthan, which involved high-tech time clocks to monitor attendance. The study’s title says it all: Band-Aids on a Corpse. E-governance can be just as bad as any other governance when the real issue is people and their motivation.
For services to improve, the people providing the services have to want to do a better job with the skills they have. A study of medical care in Delhi found that even though providers, in the public sector had much better skills than private sector providers their provision of care in actual practice was much worse.
In implementation-intensive services the key to success is face-to-face interactions between a teacher, a nurse, a policeman, an extension agent and a citizen. This relationship is about power. Amartya Sen’s report on education in West Bengal had a supremely telling anecdote in which the villagers forced the teacher to attend school, but then, when the parents went off to work, the teacher did not teach, but forced the children to massage his feet. As long as the system empowers providers over citizens, technology is irrelevant.
The answer to successfully providing basic services is to create systems that provide both autonomy and accountability. In basic education for instance, the answer to poor teaching is not controlling teachers more. The key is to hire teachers who want to teach and let them teach, expressing their professionalism and vocation as a teacher through autonomy in the classroom. This autonomy has to be matched with accountability for results—not just narrowly measured through test scores, but broadly for the quality of the education they provide.
A recent study in Uttar Pradesh showed that if, somehow, all civil service teachers could be replaced with contract teachers, the state could save a billion dollars a year in revenue and double student learning. Just the additional autonomy and accountability of contracts through local groups—even without complementary system changes in information and empowerment—led to that much improvement. The first step to being part of the solution is to create performance information accessible to those outside of the government.
In the context of the passage, we can infer that the title “Band Aids on a Corpse” (in paragraph 2) suggests that:
Video Explanation
Explanatory Answer
According to the author, service delivery in Indian education can be improved in all of the following ways EXCEPT through:
Video Explanation
Explanatory Answer
Which of the following, IF TRUE, would undermine the passage’s main argument?
Video Explanation
Explanatory Answer
The author questions the use of monitoring systems in services that involve face-to-face interaction between service providers and clients because such systems:
Video Explanation
Explanatory Answer
The main purpose of the passage is to:
Video Explanation
Explanatory Answer
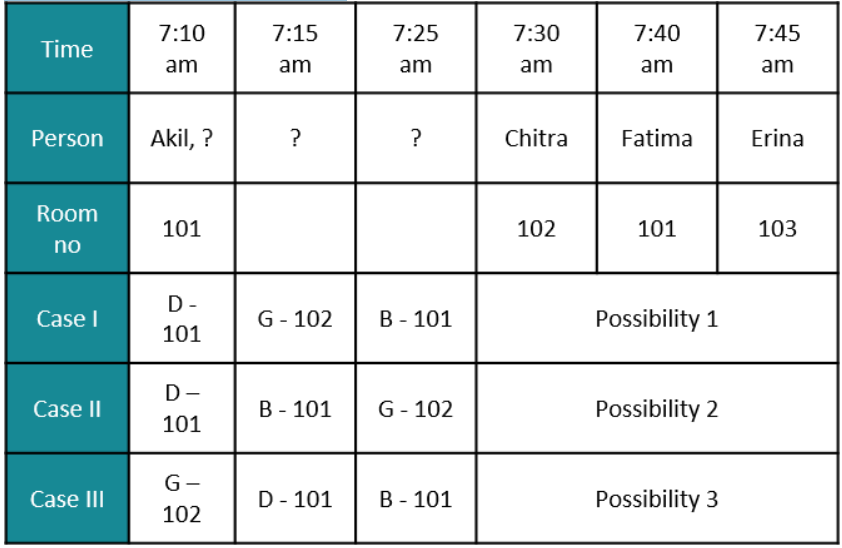
If Ganeshan entered the venue before Divya, when did Balaram enter the venue?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
If Ganeshan entered the venue before Divya, we are looking at possibility 3 from the table.
Therefore Balaram entered the venue at 7:25 am
When did Erina reach the venue?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
From the table, we can see that Erina was the last one to reach i.e. at 7:45 am.
Who else was in Room 102 when Ganeshan entered?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
Ganeshan was the first to enter room 102. Therefore no one was there before Ganeshan entered
room 102.
What best can be said about the room to which Divya was allotted?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
From the above table, we can see that Divya is definitely in room 101.
Job Interview
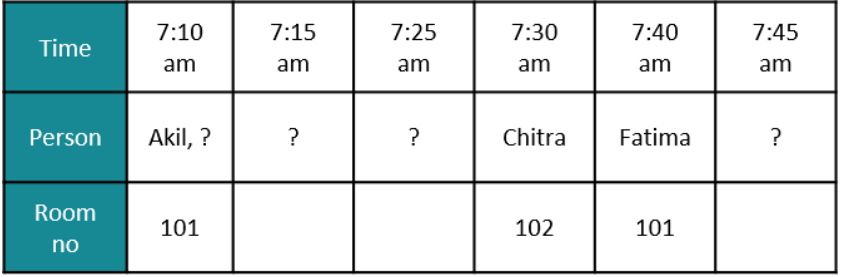
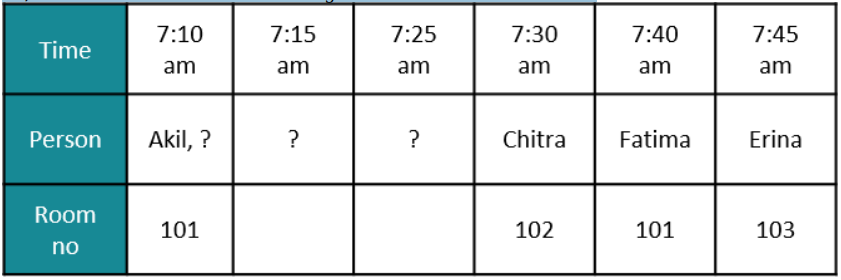
Seven candidates, Akil, Balaram, Chitra, Divya, Erina, Fatima, and Ganeshan, were invited to interview for a position. Candidates were required to reach the venue before 8 am. Immediately upon arrival, they were sent to one of three interview rooms: 101, 102, and 103. The following venue log shows the arrival times for these candidates. Some of the names have not been recorded in the log and have been marked as ‘?’.
Additionally here are some statements from the candidates:
Balaram: I was the third person to enter Room 101.
Chitra: I was the last person to enter the room I was allotted to.
Erina: I was the only person in the room I was allotted to.
Fatima: Three people including Akil were already in the room that I was allotted to when I entered it.
Ganeshan: I was one among the two candidates allotted to Room 102.
What best can be said about the room to which Divya was allotted?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
From the above table, we can see that Divya is definitely in room 101.
Who else was in Room 102 when Ganeshan entered?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
Ganeshan was the first to enter room 102. Therefore no one was there before Ganeshan entered
room 102.
When did Erina reach the venue?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
From the table, we can see that Erina was the last one to reach i.e. at 7:45 am.
If Ganeshan entered the venue before Divya, when did Balaram enter the venue?
Video Explanation
Explanatory Answer
Look at the statements given by Erina and Ganeshan.
Think about the number of candidates in the rooms.
One room has only one candidate, one room has 2 candidates, so the third room should have 4
candidates.
So, number of candidates should be distributed as 4, 2, 1.
But which room has 2 candidates and which one has 4?
Room number 102 has 2 candidates. G plus one more. Balaram was the third one to enter 101, so
101 should have had at least 3 candidates.
This implies 103 has only one candidate.
Fatima is the 4th one into a room. What does this mean? Akhil should also be in the same room as
Fatima.
A, B and F go to room number 101. C should go to 102, E should go to 103.
Fatima is the 4th one into a room. Chitra is the last to enter her room.
So, the one at 7:45 should be entering a different room. Who is this?
A, B and F go to room number 101. C should go to 102, E should go to 103. E should be the one
who goes at 7:45 am.
We have B, D and G remaining. B and D go into 101, G goes to 102. B comes after D as B is the
third to go into 101.
Write down the different combinations.
7:10, 7:15 and 7:25 could be D, B, G or D, G, B or G, D, B.
Let us move on to questions.
If Ganeshan entered the venue before Divya, we are looking at possibility 3 from the table.
Therefore Balaram entered the venue at 7:25 am
Which of the following statements MUST be FALSE?
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
Let us go statement-by-statement and see if we can find some easy one that HAS to be FALSE.
(A) The numbers of Gold and Platinum tickets bought by Young visitors were equal.
YNG-PT = YNG-GOLD. These two should add up to 42. Or, both should be 21. Total PT should be
42. Total GOLD should be 43.
All of these appear to be possible. Let us look at the other choices and see if we can find an easier
CLEARLY FALSE statement.
Else, we will revisit this.
(B) The numbers of Middle-aged and Young visitors buying Gold tickets were equal.
MID-GOLD = YNG-GOLD. MID-GOLD should also be 42 – y. This tells us that z should be 1. This
also appears prima-facie possible.
Let us look at the others also before we revisit this one and completely fill the grid.
(C) The numbers of Old and Middle-aged visitors buying Economy tickets were equal.
OLD-ECO = MID-ECO.These two should add up to 17 so these two CANNOT be equal.
So, statement C is DEFINITELY FALSE.
(D) The numbers of Old and Middle-aged visitors buying Platinum tickets were equal.
OLD-PT = MID-PT. Both of these should be y2𝑦2. This also appears to be alright.
If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Economy tickets, then the number of Old visitors buying Gold tickets was [TITA]
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-PT = MID-ECO. MID-ECO = 17 – z or, OLD-PT = 17 – z.
17 – z = - 20 – 2z. Or, z = 3.
If the number of Old visitors buying Gold tickets was strictly greater than the number of Young visitors buying Gold tickets, then the number Middle-aged visitors buying Gold tickets was [TITA]
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-GOLD > YNG-GOLD.
Z > 42 – y Or, y + z > 42
We need to find MID-GOLD. This is equal to 85 – 2y – z – (42 – y) = 43 – (y + z).
We know that y + z > 42. So, MID-GOLD has to be 0.
If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Platinum tickets, then which among the following could be the total number of Platinum tickets sold?
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-PT should be equal to MID-PT, OLD-PT and MID-PT add up to y.
So, each should be y2𝑦2. Now, we know that y2𝑦2 = 20 – 2z.
Total number of PT seats = 2y = 4 (20 – 2z) = 8 (10 – z). So, this number should be a multiple of 8.
The only possible answer is 32
Amusement Park Tickets
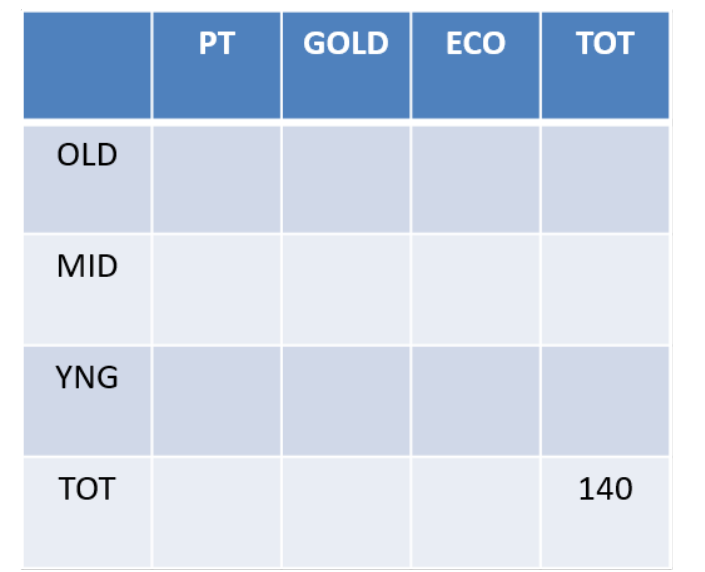
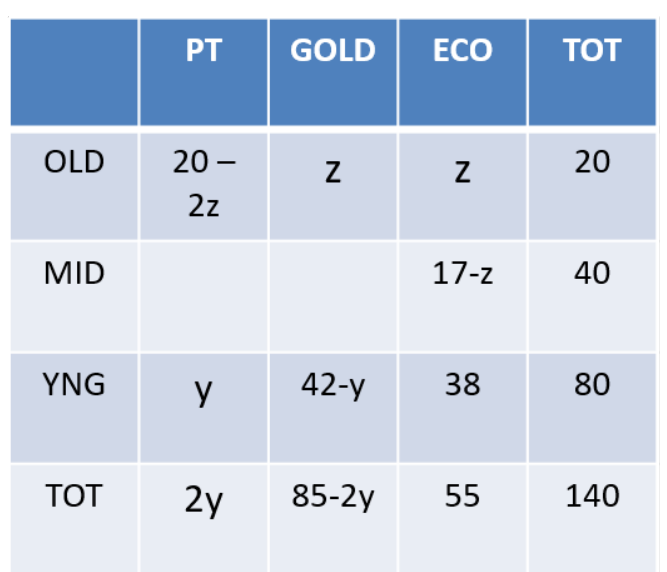
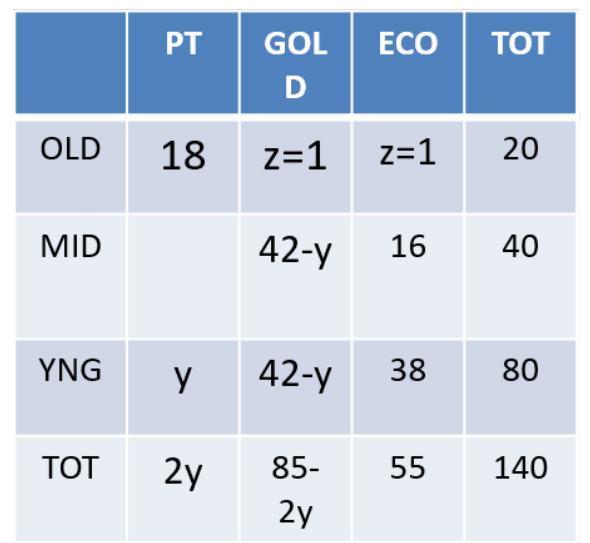
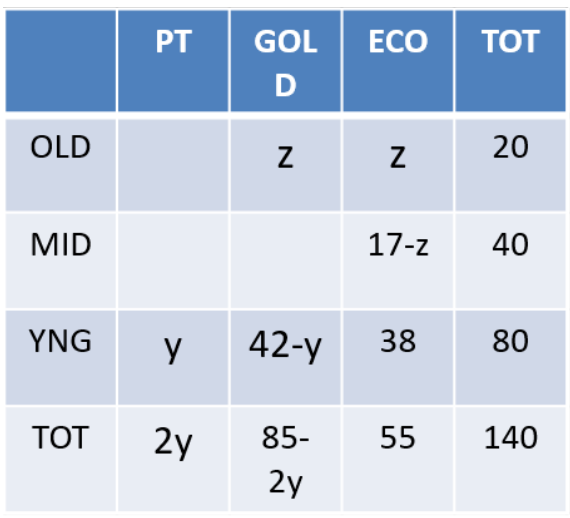
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Platinum tickets, then which among the following could be the total number of Platinum tickets sold?
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-PT should be equal to MID-PT, OLD-PT and MID-PT add up to y.
So, each should be y2𝑦2. Now, we know that y2𝑦2 = 20 – 2z.
Total number of PT seats = 2y = 4 (20 – 2z) = 8 (10 – z). So, this number should be a multiple of 8.
The only possible answer is 32
If the number of Old visitors buying Gold tickets was strictly greater than the number of Young visitors buying Gold tickets, then the number Middle-aged visitors buying Gold tickets was [TITA]
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-GOLD > YNG-GOLD.
Z > 42 – y Or, y + z > 42
We need to find MID-GOLD. This is equal to 85 – 2y – z – (42 – y) = 43 – (y + z).
We know that y + z > 42. So, MID-GOLD has to be 0.
If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Economy tickets, then the number of Old visitors buying Gold tickets was [TITA]
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
OLD-PT = MID-ECO. MID-ECO = 17 – z or, OLD-PT = 17 – z.
17 – z = - 20 – 2z. Or, z = 3.
Which of the following statements MUST be FALSE?
Video Explanation
Explanatory Answer
From second constraint,
OLD Visitors = x, MID = 2x, Young = 4x.
7x = 140 or, x = 20 , 2x = 40 , 4x = 80.
Let us fill this in. and then go to constraint 3 and 4.
From constraint 3, Total Platinum = 2y, then YNG platinum should be y.
From constraint 4, Let us fill OLD-GOLD and OLD-ECO has z.
Let us go statement-by-statement and see if we can find some easy one that HAS to be FALSE.
(A) The numbers of Gold and Platinum tickets bought by Young visitors were equal.
YNG-PT = YNG-GOLD. These two should add up to 42. Or, both should be 21. Total PT should be
42. Total GOLD should be 43.
All of these appear to be possible. Let us look at the other choices and see if we can find an easier
CLEARLY FALSE statement.
Else, we will revisit this.
(B) The numbers of Middle-aged and Young visitors buying Gold tickets were equal.
MID-GOLD = YNG-GOLD. MID-GOLD should also be 42 – y. This tells us that z should be 1. This
also appears prima-facie possible.
Let us look at the others also before we revisit this one and completely fill the grid.
(C) The numbers of Old and Middle-aged visitors buying Economy tickets were equal.
OLD-ECO = MID-ECO.These two should add up to 17 so these two CANNOT be equal.
So, statement C is DEFINITELY FALSE.
(D) The numbers of Old and Middle-aged visitors buying Platinum tickets were equal.
OLD-PT = MID-PT. Both of these should be y2𝑦2. This also appears to be alright.
If the smallest box on the grid is equivalent to revenue of Rs.1 crore, then what approximately was the total revenue of Bravo in Rs. crore?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
Bravo’s revenues are from 7 companies.
In No-hope, the revenues should be Rs. 4 Crores.
In Blockbuster, the revenues should be 4 + 6 = Rs. 10 Crores.
In Promising, the revenues should be Rs. 2 Crores.(this could be 3)
In Doubtful, the revenues should be 9 + 6 + 2 = Rs. 17 Crores.
This adds up to Rs. 33 crores.
The answer choice should be C.
Which of the following statements is NOT correct?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
A) Alfa Block Buster revenues = 9 squares. Charlie Promising Revenues = 9 square units. This is
correct.
B) Bravo Blockbuster = 10 squares, Alfa doubtful = 12 squares.This is not correct.
C) No-Hope = 15 squares, Doubtful = 29 squares. This is correct.
D) Given in the question. This is correct.
Which of the following is the correct sequence of numbers of products Bravo had in No-hope, Doubtful, Promising and Blockbuster categories respectively?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
From the table we can see that Choice B 1,3,1,2 is the correct sequence of no. of products.
Considering all companies products, which product category had the highest revenue?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
It is between Blockbuster and Doubtful. Doubtful has two small squares whereas everything in
Blockbuster is sizable. Therefore Blockbuster had the highest revenue.
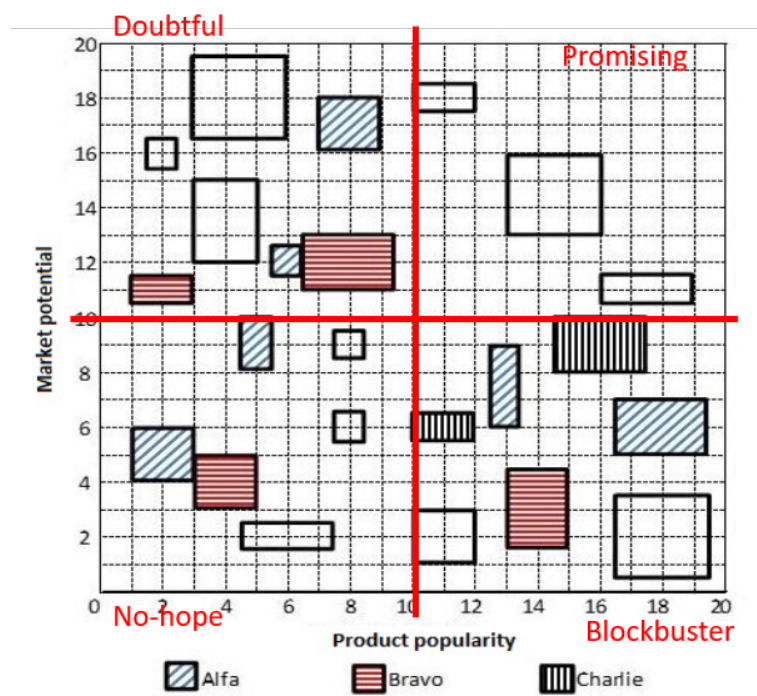
Products and Companies
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.
The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:
The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Considering all companies products, which product category had the highest revenue?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
It is between Blockbuster and Doubtful. Doubtful has two small squares whereas everything in
Blockbuster is sizable. Therefore Blockbuster had the highest revenue.
Which of the following is the correct sequence of numbers of products Bravo had in No-hope, Doubtful, Promising and Blockbuster categories respectively?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
From the table we can see that Choice B 1,3,1,2 is the correct sequence of no. of products.
Which of the following statements is NOT correct?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
A) Alfa Block Buster revenues = 9 squares. Charlie Promising Revenues = 9 square units. This is
correct.
B) Bravo Blockbuster = 10 squares, Alfa doubtful = 12 squares.This is not correct.
C) No-Hope = 15 squares, Doubtful = 29 squares. This is correct.
D) Given in the question. This is correct.
If the smallest box on the grid is equivalent to revenue of Rs.1 crore, then what approximately was the total revenue of Bravo in Rs. crore?
Video Explanation
Explanatory Answer
The companies classified their products into four categories based on a combination of scores (out
of 20) on the two parameters - Product popularity and Market potential as given below
From condition 1, Alfa and Bravo should have 2 each, Charlie should have 3.
From condition 2, Bravo = 1, Charlie = 2, Alfa = 3.
From condition 3, Alfa = Bravo = Charlie = 1.
From condition 4, Alpha = 4, Bravo = 3, Charlie = 0.
Let us capture this differently and then take it from there.
From condition 5, The big free square is Bravo.
From condition 6, The big free square is Charlie.
From condition 7, Charlie has rectangle and Square.
From condition 8, Chances are the big square in Promising is Charlie’s.
Bravo’s revenues are from 7 companies.
In No-hope, the revenues should be Rs. 4 Crores.
In Blockbuster, the revenues should be 4 + 6 = Rs. 10 Crores.
In Promising, the revenues should be Rs. 2 Crores.(this could be 3)
In Doubtful, the revenues should be 9 + 6 + 2 = Rs. 17 Crores.
This adds up to Rs. 33 crores.
The answer choice should be C.
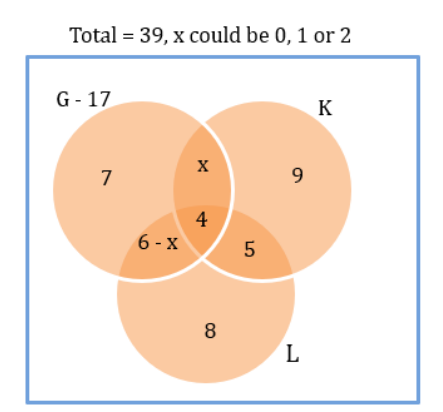
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and L?
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram. 
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
The other three should have opted out of one or the other of G and L. Let us assume m students
left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and L = 7 – x = 6.
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K? [TITA]
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
We know that G ∩ K ∩ L = 0. We know that the 4 that were originally here are distributed among
the three regions currently having x, 6 – x and 5.
We know that one student leaves K. So, this student should have gone to the region (G and L but
not K).
Or, (G and L but not K) will now read 7 – x.
The other three should have opted out of one or the other of G and L. Let us assume m students
left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and K = 3 + x – m. 3 + 1 -2 = 2.
If the numbers of students enrolled in K and L are in the ratio 19:22, then what is the number of students enrolled in L?
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
Ratio of K : L = 19 : 22. or, x = 1.
Or, number of students in L = 22.
What is the minimum number of students enrolled in both G and L but not in K? [TITA]
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
For 6 - x to be minimum, x should be maximum i.e. x should take 2.
Therefore the minimum number of students enrolled in both G and L but not in K is 4.
Fun Sports Club
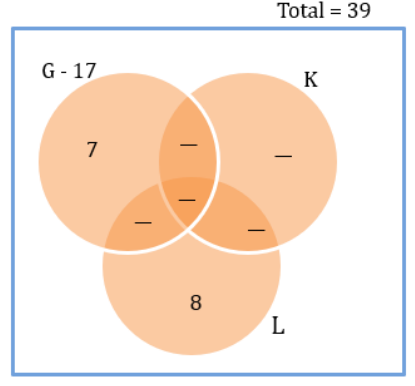
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
What is the minimum number of students enrolled in both G and L but not in K? [TITA]
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
For 6 - x to be minimum, x should be maximum i.e. x should take 2.
Therefore the minimum number of students enrolled in both G and L but not in K is 4.
If the numbers of students enrolled in K and L are in the ratio 19:22, then what is the number of students enrolled in L?
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
Ratio of K : L = 19 : 22. or, x = 1.
Or, number of students in L = 22.
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K? [TITA]
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
We know that G ∩ K ∩ L = 0. We know that the 4 that were originally here are distributed among
the three regions currently having x, 6 – x and 5.
We know that one student leaves K. So, this student should have gone to the region (G and L but
not K).
Or, (G and L but not K) will now read 7 – x.
The other three should have opted out of one or the other of G and L. Let us assume m students
left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and K = 3 + x – m. 3 + 1 -2 = 2.
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and L?
Video Explanation
Explanatory Answer
From condition 3, we get the above diagram
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.
From condition 1, we get the above diagram.
From condition 6, we can get the diagram.
From condition 4, we get the above diagram.
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < 5252.
x could be 0, 1 or 2.
The other three should have opted out of one or the other of G and L. Let us assume m students
left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and L = 7 – x = 6.
The complete list of brands whose profits went up in 2017 from 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that the profits of Azra, Bysi, Dipq went up in 2017 from 2016.
The brand that had the highest profit in 2017 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Bysi had the highest profit in 2017.
The brand that had the highest profit in 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Cxqi had the highest profit in 2016.
The brand that had the highest revenue in 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Azra had the highest revenue in 2016.
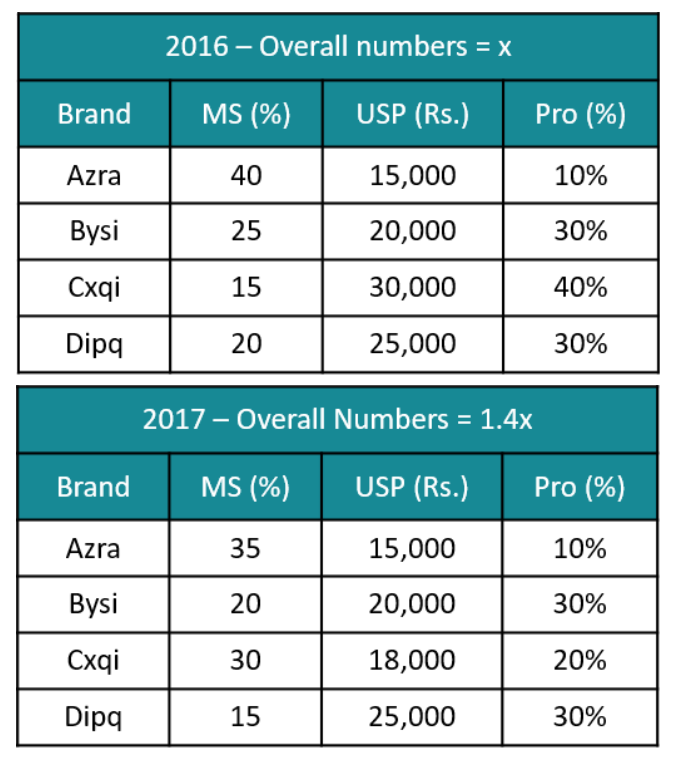
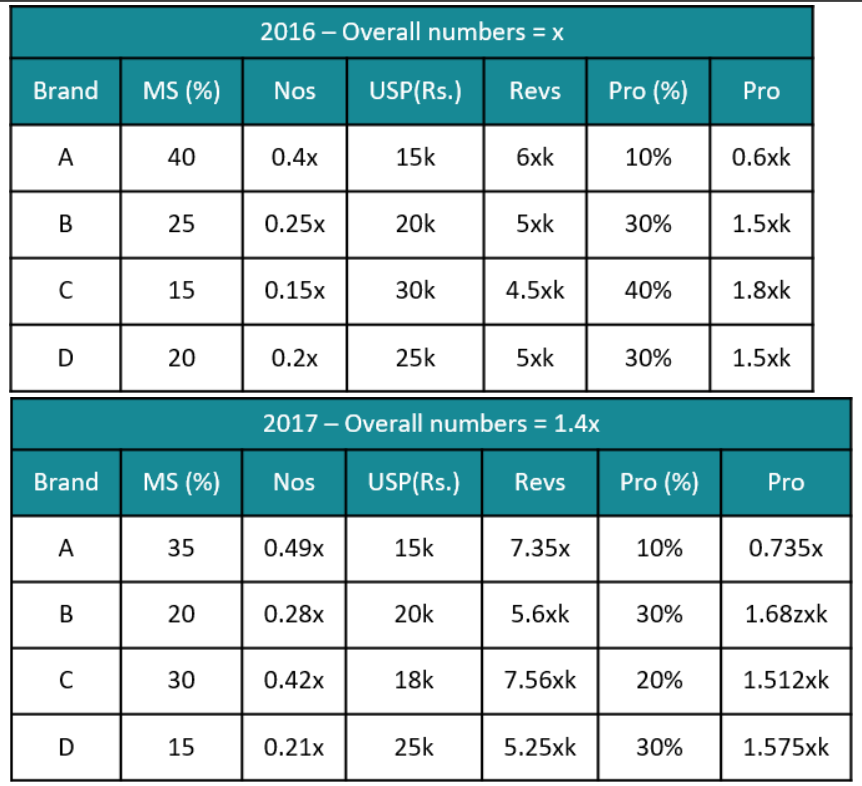
Smartphones
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:
In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
The brand that had the highest revenue in 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Azra had the highest revenue in 2016.
The brand that had the highest profit in 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Cxqi had the highest profit in 2016.
The brand that had the highest profit in 2017 is:
Video Explanation
Explanatory Answer
From the above table, we can see that Bysi had the highest profit in 2017.
The complete list of brands whose profits went up in 2017 from 2016 is:
Video Explanation
Explanatory Answer
From the above table, we can see that the profits of Azra, Bysi, Dipq went up in 2017 from 2016.
How many colleges have overall scores between 31 and 40, both inclusive?
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
From the above table, we can see that the number of colleges which have overall scores between
31 and 40 both inclusive is 0.
What is the highest overall score among the eight colleges? [TITA]
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
From the above table, we can see that the highest overall score among the eight colleges is 48.
