Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
How many countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh?
Video Explanation

How many countries in the ROW were visited by both Nitesh and Samantha?
Video Explanation

How many countries in Europe were visited only by Nitesh?
Video Explanation

How many countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh?
Video Explanation

The chart below provides complete information about the number of countries visited by Dheeraj, Samantha
and Nitesh, in Asia, Europe and the rest of the world (ROW).
The following additional facts are known about the countries visited by them.
1. 32 countries were visited by at least one of them.
2. USA (in ROW) is the only country that was visited by all three of them.
3. China (in Asia) is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha.
4. France (in Europe) is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not
by Nitesh.
5. Half of the countries visited by both Samantha and Nitesh are in Europe.
How many countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh?
Video Explanation

How many countries in Europe were visited only by Nitesh?
Video Explanation

How many countries in the ROW were visited by both Nitesh and Samantha?
Video Explanation

How many countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh?
Video Explanation

What is the maximum possible voting margin with which one of the candidates can win?
Video Explanation

If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is
guaranteed to get?
Video Explanation

If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can
get?
Video Explanation

What is the minimum percentage of students who will vote in the election?
Video Explanation

If both of them run staid campaigns attacking the other, then what percentage of students will vote in the
election?
Video Explanation

Two students, Amiya and Ramya are the only candidates in an election for the position of class representative.
Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns
they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous
campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
• The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the
two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2+2)%, that is, 80% of
the students will vote in the election.
• Among voting students, the percentage of votes for each candidate will be proportional to the levels of their
campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2)
campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3. The abovementioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
• If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the
students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have
otherwise voted for Amiya, will not vote at all.
• If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the
students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have
otherwise voted for Ramya, will not vote at all.
• If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for
them had they run campaigns focusing on issues, will not vote at all
If both of them run staid campaigns attacking the other, then what percentage of students will vote in the
election?
Video Explanation

What is the minimum percentage of students who will vote in the election?
Video Explanation

If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can
get?
Video Explanation

If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is
guaranteed to get?
Video Explanation

What is the maximum possible voting margin with which one of the candidates can win?
Video Explanation

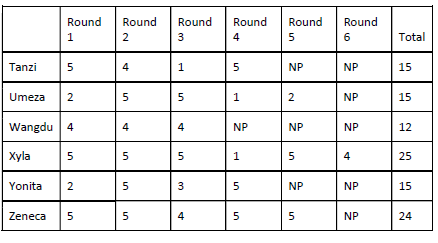
What is the number of the team that played Team 6 in Round 3?
Video Explanation

What is the number of the team that played Team 1 in Round 7?
Video Explanation

Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
Video Explanation

What is the number of the team that played Team 1 in Round 5?
Video Explanation

How many rounds were there in the tournament?
Video Explanation

The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET
tournament. These teams are divided equally into two groups. In the tournament, each team plays every other
team in the same group only once, and each team in the other group exactly twice. The tournament has several
rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In
Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
How many rounds were there in the tournament?
How many rounds were there in the tournament?
Video Explanation

What is the number of the team that played Team 1 in Round 5?
Video Explanation

Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
Video Explanation

What is the number of the team that played Team 1 in Round 7?
Video Explanation

What is the number of the team that played Team 6 in Round 3?
Video Explanation

Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by D from O
Video Explanation

How many surfers distributed their stars among exactly 2 bloggers?
Video Explanation

What was the number of stars received by D from Y?
Video Explanation

What was the total number of stars received by D?
Video Explanation

Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D.
The number of stars received by A and B from the six web surfers is shown in the figure below.
The following additional facts are known regarding the number of stars received by the bloggers from the
surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y.
What was the total number of stars received by D?
Video Explanation

What was the number of stars received by D from Y?
Video Explanation

How many surfers distributed their stars among exactly 2 bloggers?
Video Explanation

Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by D from O
Video Explanation

What would have been the percentage wealth gain for a trader, who bought equal numbers of all bullish
shares at opening price and sold them at their day’s high?
Video Explanation

Daily loss for a share is defined as (Opening price - Closing price) / (Opening price). Which among the
shares A, B, F and G had the highest daily loss on that day?
Video Explanation

The chart below shows the price data for seven shares - A, B, C, D, E, F, and G as a candlestick plot for a
particular day. The vertical axis shows the price of the share in rupees. A share whose closing price (price at the
end of the day) is more than its opening price (price at the start of the day) is called a bullish share; otherwise, it
is called a bearish share. All bullish and bearish shares are shown in green and red colour respectively.
Daily loss for a share is defined as (Opening price - Closing price) / (Opening price). Which among the
shares A, B, F and G had the highest daily loss on that day?
Video Explanation

What would have been the percentage wealth gain for a trader, who bought equal numbers of all bullish
shares at opening price and sold them at their day’s high?
Video Explanation

What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
Video Explanation

Which of the following options best describes the number of vacant houses in Row-2?
Video Explanation

Which of the following houses are definitely occupied?
Video Explanation

How many houses are vacant in Block XX?
Video Explanation

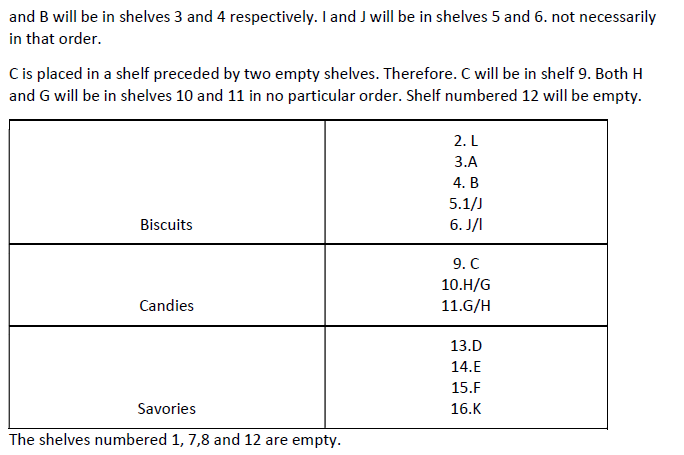
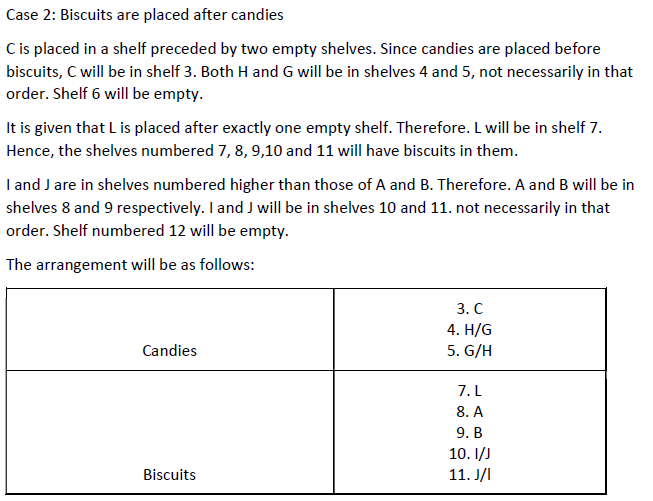
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.
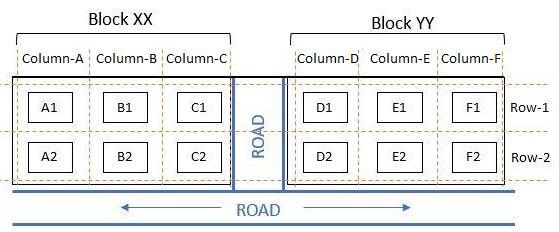
Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
How many houses are vacant in Block XX?
Video Explanation

Which of the following houses are definitely occupied?
Video Explanation

Which of the following options best describes the number of vacant houses in Row-2?
Video Explanation

What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
Video Explanation

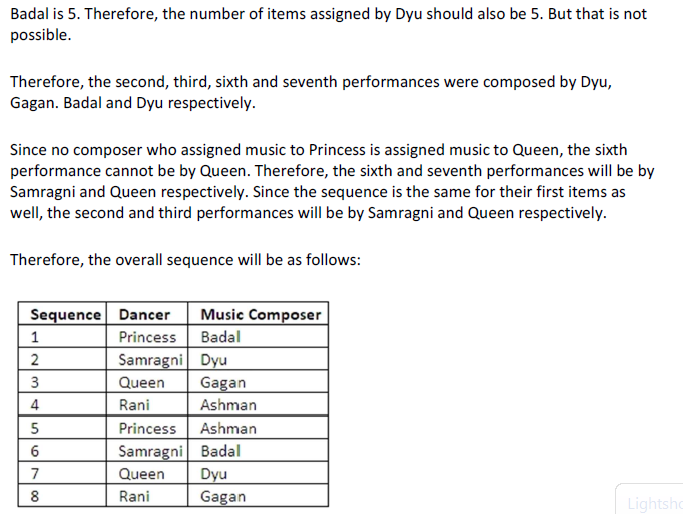
Which pair of performances were composed by the same composer?
Video Explanation

Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Which pair of performances were composed by the same composer?
Video Explanation

Which among the digits 4, 6, 7 and 8 cannot be represented by the letter G?
Video Explanation

Which digit does the letter B represent?
Video Explanation


Which digit does the letter A represent?
Video Explanation

Which digit does the letter B represent?
Video Explanation

Which among the digits 3, 4, 6 and 7 cannot be represented by the letter D?
Video Explanation

Which among the digits 4, 6, 7 and 8 cannot be represented by the letter G?
Video Explanation

Which digit does the letter A represent?
Video Explanation

Which among the digits 3, 4, 6 and 7 cannot be represented by the letter D?
Video Explanation

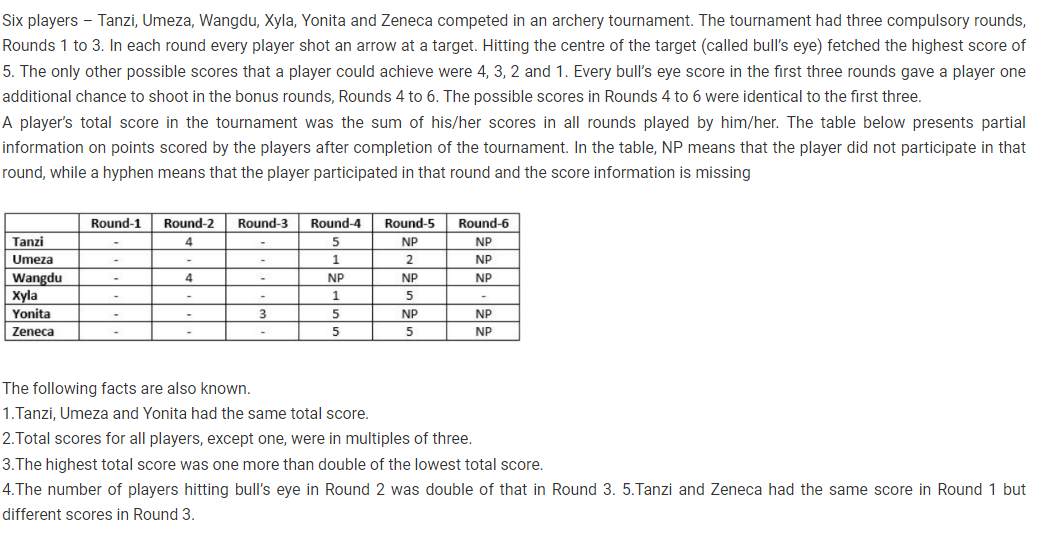
Which of the following statements is necessarily true?
Video Explanation

In how many different ways can the items be arranged on the shelves?
Video Explanation

Previous year papers
2024
2023
2022
2021
2020
2019
2018