Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
What best can be concluded about the code for the letter B?
Video Explanation

If Ganeshan entered the venue before Divya, when did Balaram enter the venue?
Video Explanation

Job Interview
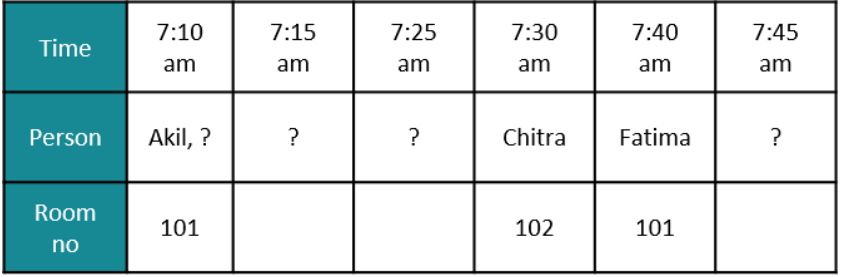
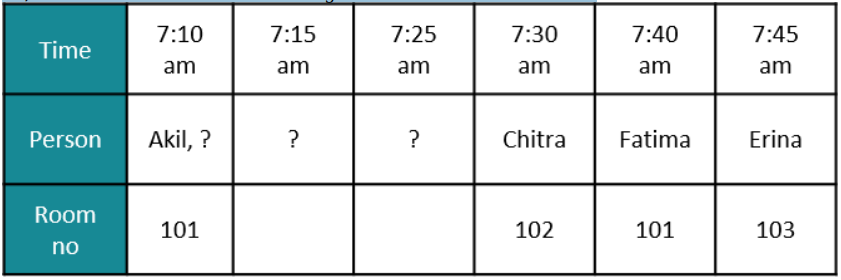
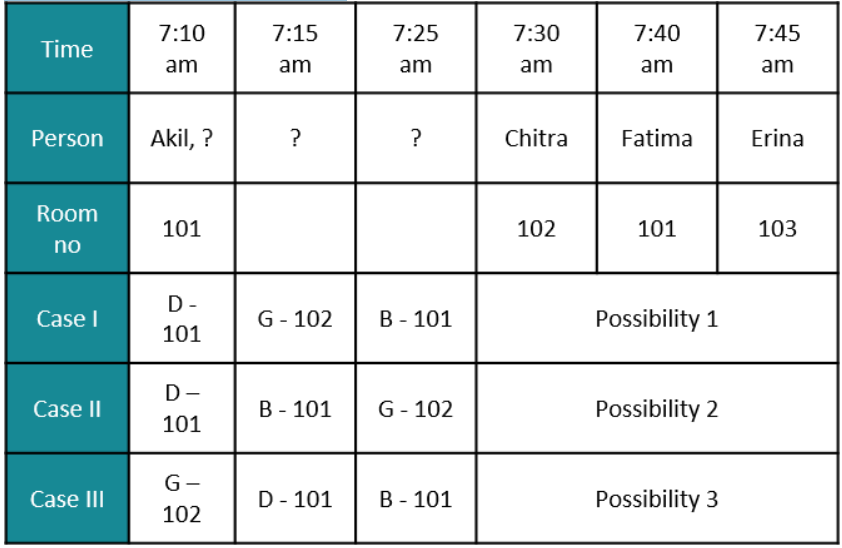
Seven candidates, Akil, Balaram, Chitra, Divya, Erina, Fatima, and Ganeshan, were invited to interview for a position. Candidates were required to reach the venue before 8 am. Immediately upon arrival, they were sent to one of three interview rooms: 101, 102, and 103. The following venue log shows the arrival times for these candidates. Some of the names have not been recorded in the log and have been marked as ‘?’.

Additionally here are some statements from the candidates:
Balaram: I was the third person to enter Room 101.
Chitra: I was the last person to enter the room I was allotted to.
Erina: I was the only person in the room I was allotted to.
Fatima: Three people including Akil were already in the room that I was allotted to when I entered it.
Ganeshan: I was one among the two candidates allotted to Room 102.
What best can be said about the room to which Divya was allotted?
Video Explanation

If Ganeshan entered the venue before Divya, when did Balaram enter the venue?
Video Explanation

What best can be said about the room to which Divya was allotted?
Video Explanation

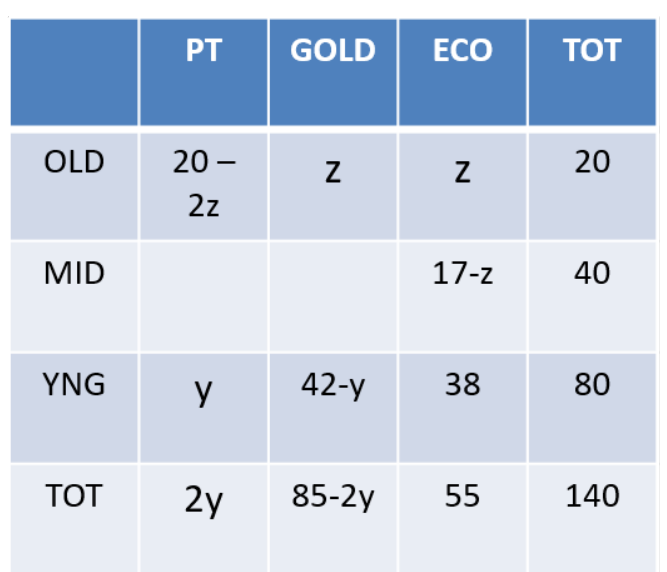
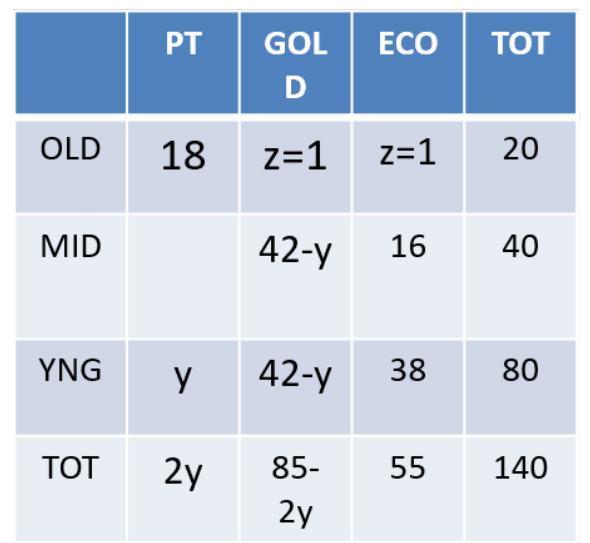
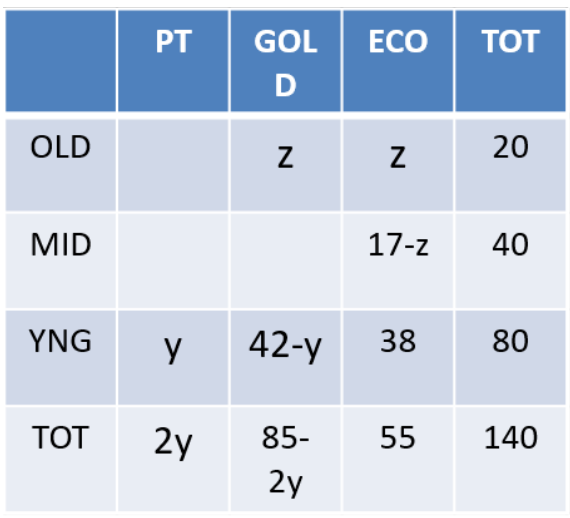
Amusement Park Tickets
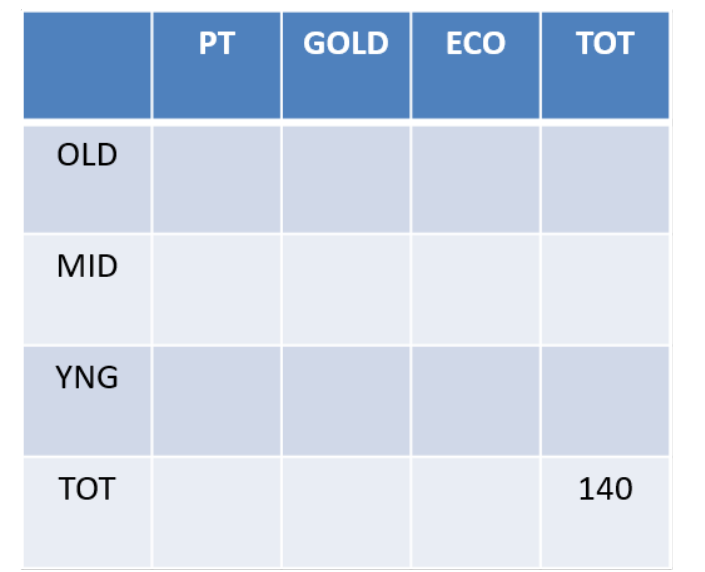
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
If the smallest box on the grid is equivalent to revenue of Rs.1 crore, then what approximately was the total revenue of Bravo in Rs. crore?
Video Explanation

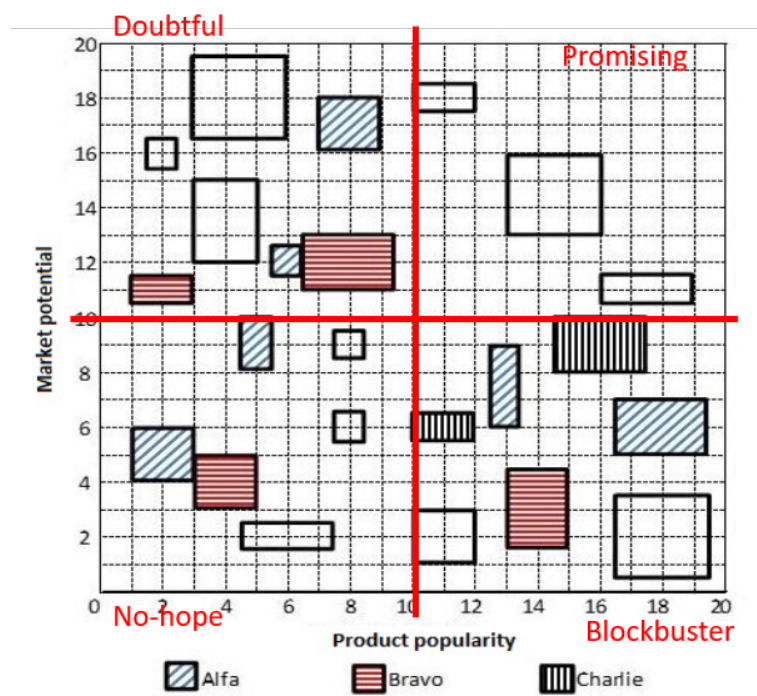
Products and Companies
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.

The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:

The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Considering all companies products, which product category had the highest revenue?
Video Explanation

Which of the following is the correct sequence of numbers of products Bravo had in No-hope, Doubtful, Promising and Blockbuster categories respectively?
Video Explanation

If the smallest box on the grid is equivalent to revenue of Rs.1 crore, then what approximately was the total revenue of Bravo in Rs. crore?
Video Explanation

Considering all companies products, which product category had the highest revenue?
Video Explanation

Which of the following is the correct sequence of numbers of products Bravo had in No-hope, Doubtful, Promising and Blockbuster categories respectively?
Video Explanation

Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and L?
Video Explanation

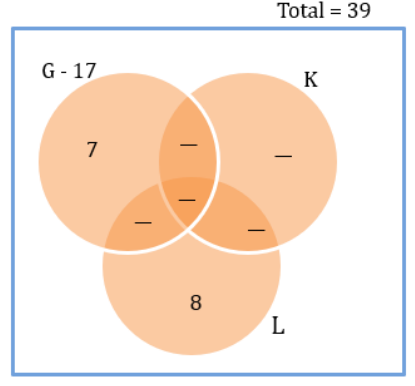
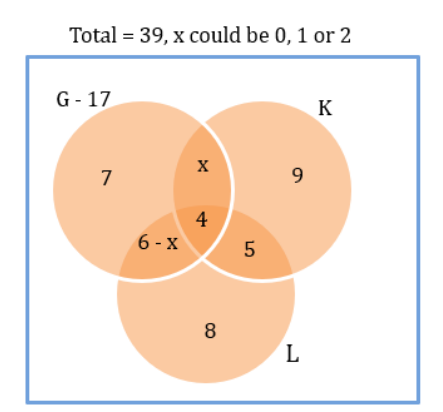
Fun Sports Club
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
What is the minimum number of students enrolled in both G and L but not in K? [TITA]
Video Explanation

If the numbers of students enrolled in K and L are in the ratio 19:22, then what is the number of students enrolled in L?
Video Explanation

Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and L?
Video Explanation

What is the minimum number of students enrolled in both G and L but not in K? [TITA]
Video Explanation

If the numbers of students enrolled in K and L are in the ratio 19:22, then what is the number of students enrolled in L?
Video Explanation

The complete list of brands whose profits went up in 2017 from 2016 is:
Video Explanation

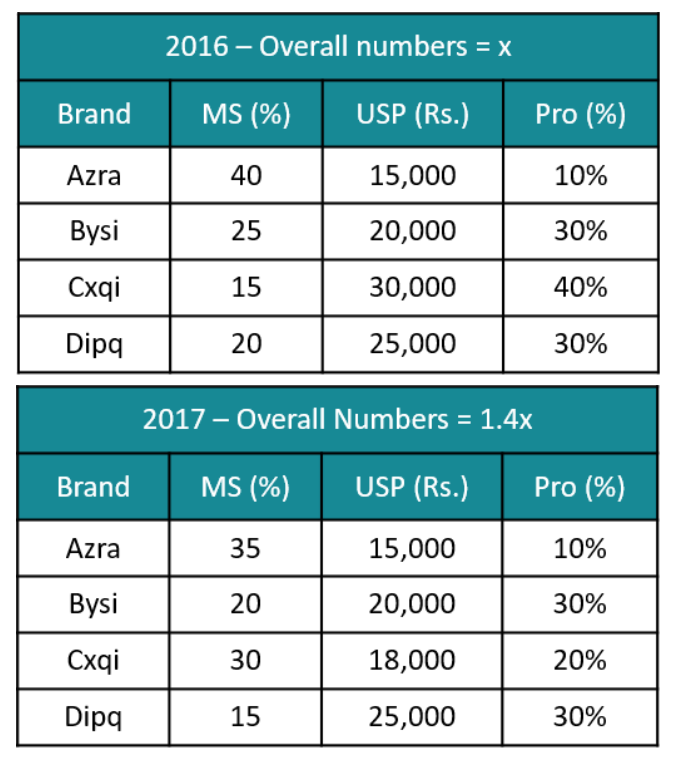
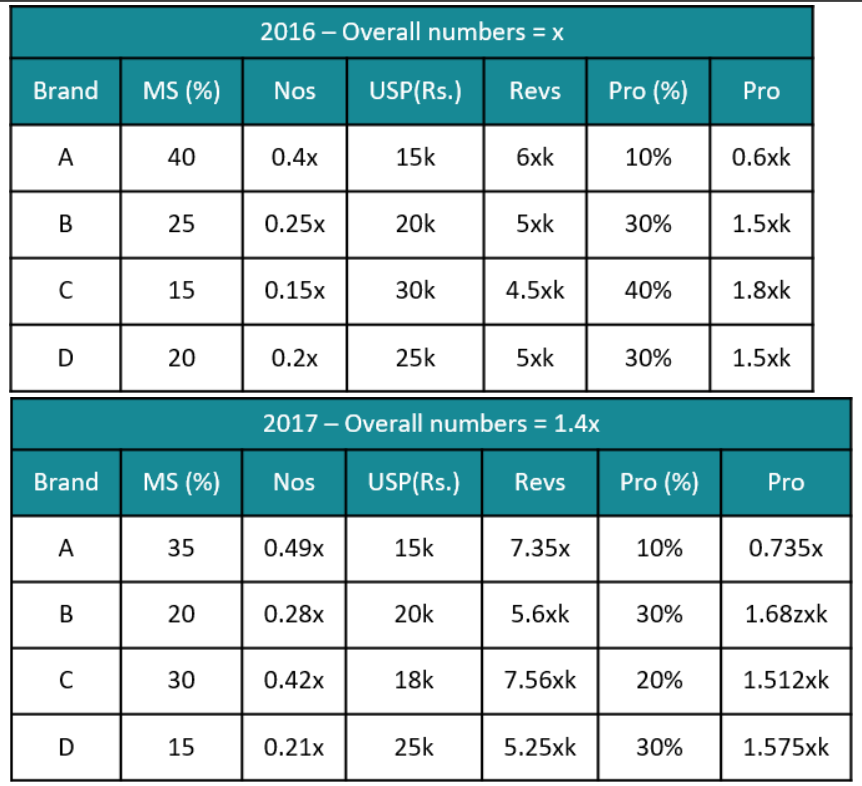
Smartphones
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:

In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
The brand that had the highest revenue in 2016 is:
Video Explanation

The complete list of brands whose profits went up in 2017 from 2016 is:
Video Explanation

The brand that had the highest revenue in 2016 is:
Video Explanation

What is the highest overall score among the eight colleges? [TITA]
Video Explanation

How many colleges have overall scores between 31 and 40, both inclusive?
Video Explanation

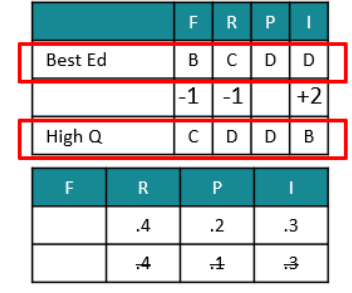
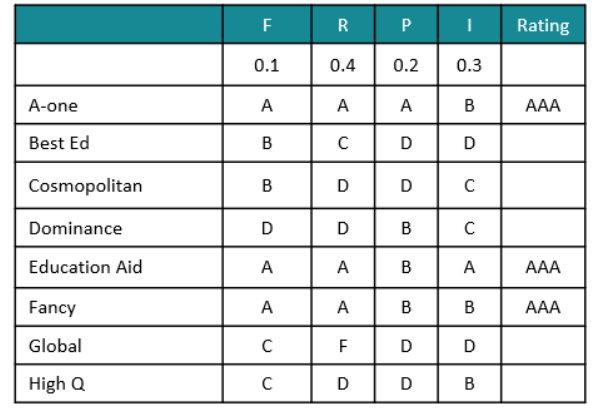
College Accreditation
An agency entrusted to accredit colleges looks at four parameters: faculty quality (F), reputation (R), placement quality (P), and infrastructure (I). The four parameters are used to arrive at an overall score, which the agency uses to give an accreditation to the colleges. In each parameter, there are five possible letter grades given, each carrying certain points: A (50 points), B (40 points), C (30 points), D (20 points), and F (0 points). The overall score for a college is the weighted sum of the points scored in the four parameters. The weights of the parameters are 0.1, 0.2, 0.3 and 0.4 in some order, but the order is not disclosed.
Accreditation is awarded based on the following scheme:

Eight colleges apply for accreditation, and receive the following grades in the four parameters (F, R, P, and I):

It is further known that in terms of overall scores:
1. High Q is better than Best Ed.
2. Best Ed is better than Cosmopolitan.
3. Education Aid is better than A-one.
What is the weight of the faculty quality parameter?
Video Explanation

How many colleges receive the accreditation of AAA? [TITA]
Video Explanation

What is the highest overall score among the eight colleges? [TITA]
Video Explanation

How many colleges have overall scores between 31 and 40, both inclusive?
Video Explanation

What is the weight of the faculty quality parameter?
Video Explanation

How many colleges receive the accreditation of AAA? [TITA]
Video Explanation

What is the minimum possible number of different types of prizes? ?
Video Explanation

What is the maximum possible number of different types of prizes?
Video Explanation

You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100. What is the maximum possible number of different types of items?
Video Explanation

A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes
What is the minimum possible number of different types of prizes? ?
Video Explanation

What is the maximum possible number of different types of prizes?
Video Explanation

You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100. What is the maximum possible number of different types of items?
Video Explanation

What was the approximate difference in profit percentages of the store in 2017 and 2018?
Video Explanation

Revenue & Cost
A large store has only three departments, Clothing, Produce, and Electronics. The following figure shows the percentages of revenue and cost from the three departments for the years 2016, 2017 and 2018. The dotted lines depict percentage levels. So for example, in 2016, 50% of store's revenue came from its Electronics department while 40% of its costs were incurred in the Produce department.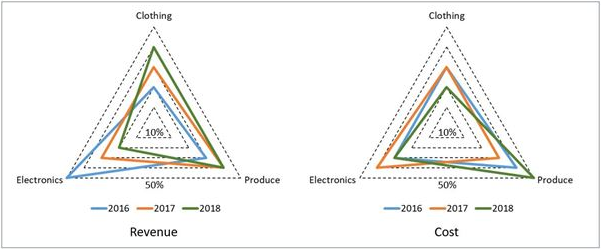
In this setup, Profit is computed as (Revenue – Cost) and Percentage Profit as Profit/Cost × 100%.
It is known that
1. The percentage profit for the store in 2016 was 100%.
2. The store’s revenue doubled from 2016 to 2017, and its cost doubled from 2016 to 2018.
3. There was no profit from the Electronics department in 2017.
4. In 2018, the revenue from the Clothing department was the same as the cost incurred in the Produce department.
What was the percentage profit of the store in 2018? [TITA]
Video Explanation

What was the ratio of revenue generated from the Produce department In 2017 to that in 2018?
Video Explanation

What percentage of the total profits for the store in 2016 was from the Electronics department? [TITA]
Video Explanation

What was the approximate difference in profit percentages of the store in 2017 and 2018?
Video Explanation

What was the percentage profit of the store in 2018? [TITA]
Video Explanation

What was the ratio of revenue generated from the Produce department In 2017 to that in 2018?
Video Explanation

What percentage of the total profits for the store in 2016 was from the Electronics department? [TITA]
Video Explanation

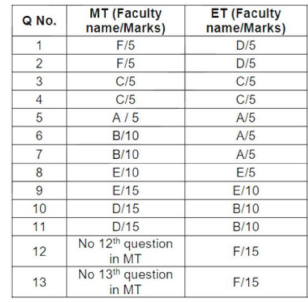
MT & ET
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
How many 5‐mark questions were there in MT and ET combined?
Video Explanation

Which of the following questions did Beti prepare in ET?
Video Explanation

How many 5‐mark questions were there in MT and ET combined?
Video Explanation

Which of the following questions did Beti prepare in ET?
Video Explanation

How many pouches contain exactly one coin? [TITA]
Video Explanation

What is the number of slots for which the average amount (in rupees) of its three pouches is an integer? [TITA]
Video Explanation

The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Video Explanation

Three pouches
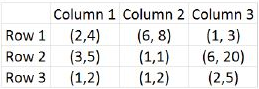
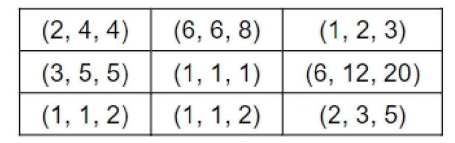
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8.
There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row? [TITA]
Video Explanation

How many pouches contain exactly one coin? [TITA]
Video Explanation

What is the number of slots for which the average amount (in rupees) of its three pouches is an integer? [TITA]
Video Explanation

The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Video Explanation

Previous year papers
2023
2022
2021
2020
2019
2018