Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
419
Learners
asked the doubt
Previous Year Questions
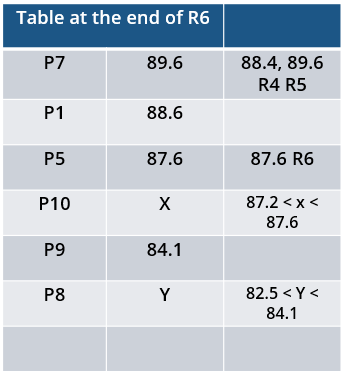
Which of the following can be the final score (in m) of P8?
Video Explanation
Explanatory Answer
By how much did the gold medalist improve his score (in m) in the second phase?
Video Explanation
Explanatory Answer
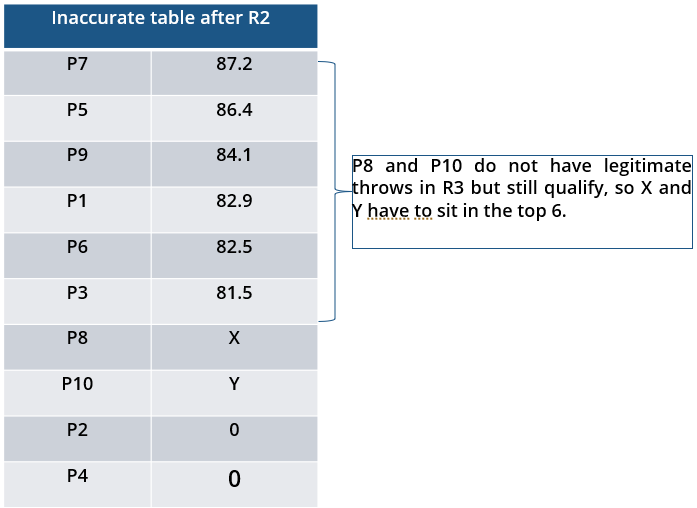
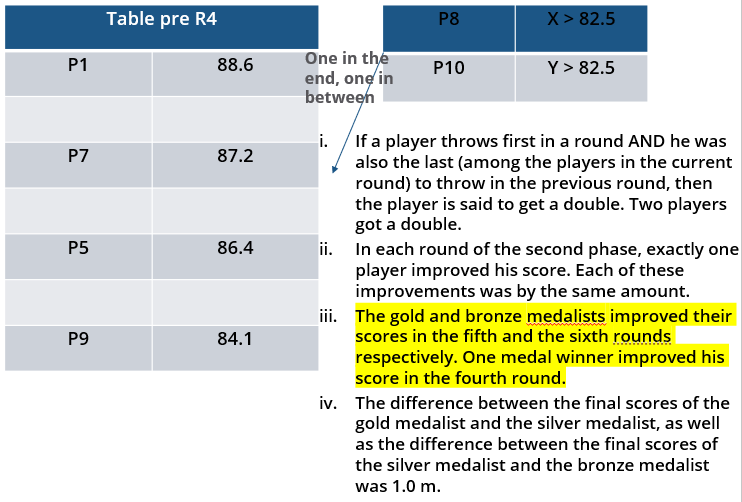
10 players – P1, P2, … , P10 - competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a 'valid' one. For an invalid throw, the distance is taken as zero. A player's score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round.
In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.
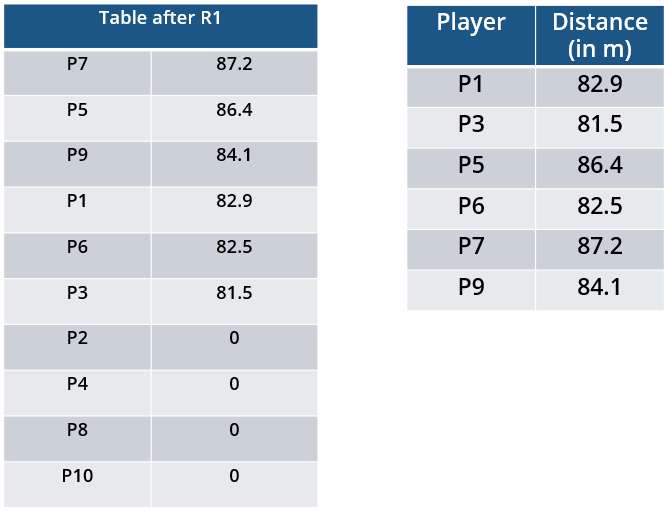
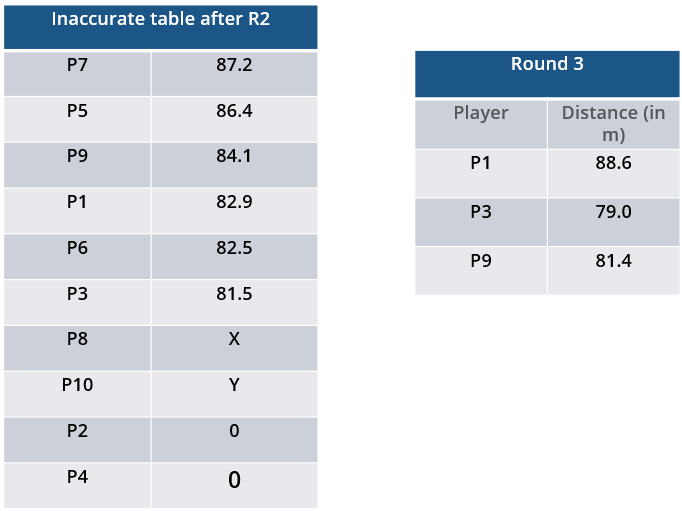
All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.
Distances covered by all the valid throws in the first round
| Player | Distance (in m) |
| P1 | 82.9 |
| P3 | 81.5 |
| P5 | 86.4 |
| P6 | 82.5 |
| P7 | 87.2 |
| P9 | 84.1 |
Distances covered by all the valid throws in the third round
| Player | Distance (in m) |
| P1 | 88.6 |
| P3 | 79.0 |
| P9 | 81.4 |
The following facts are also known.
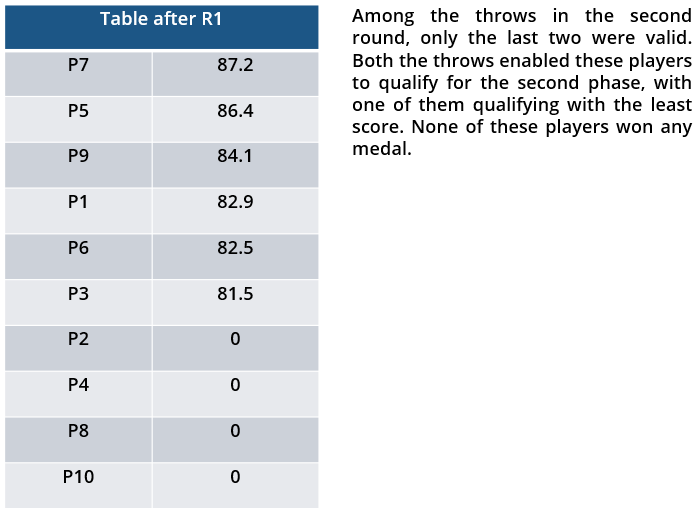
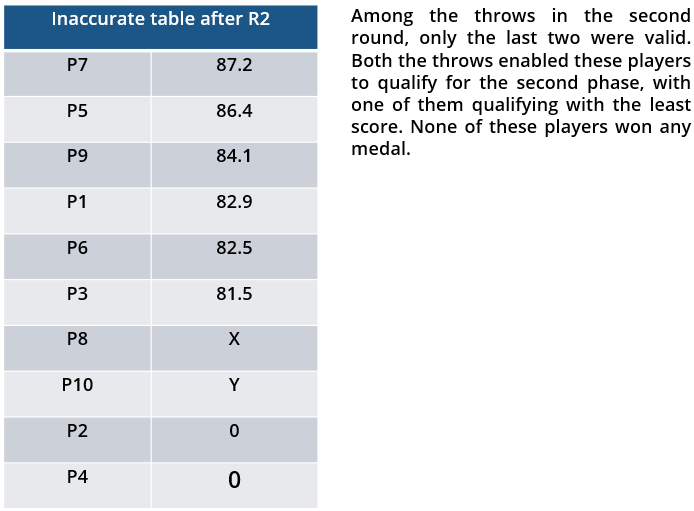
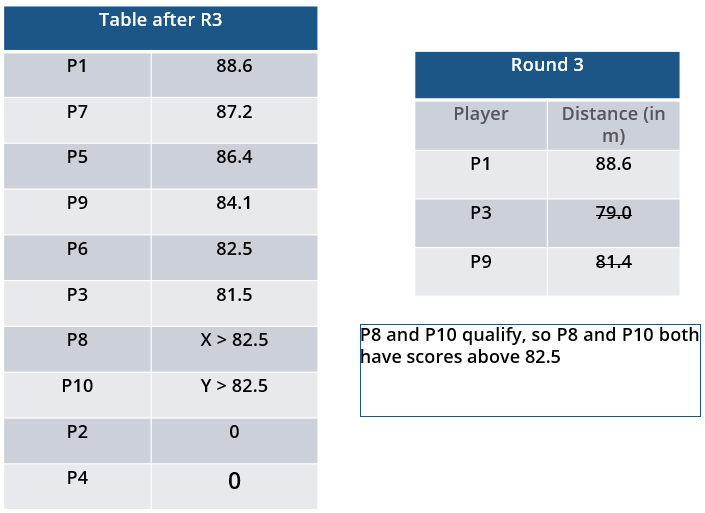
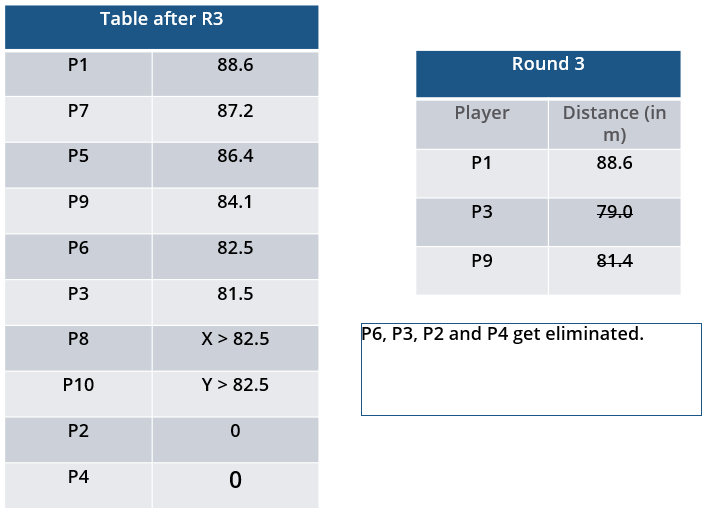
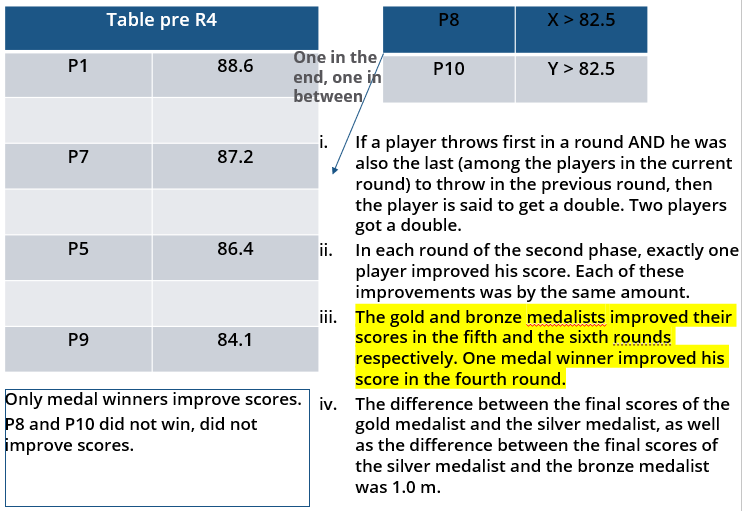
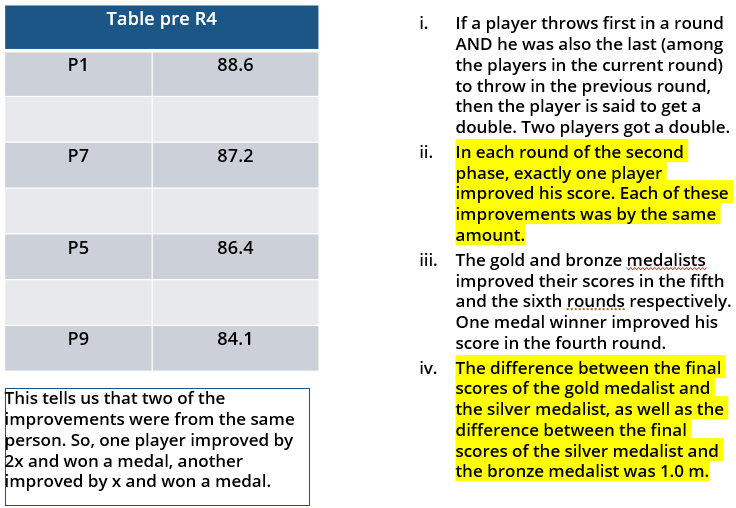
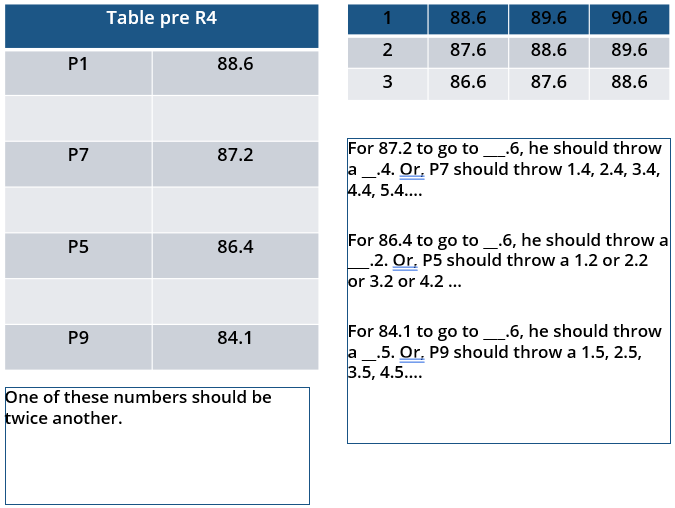
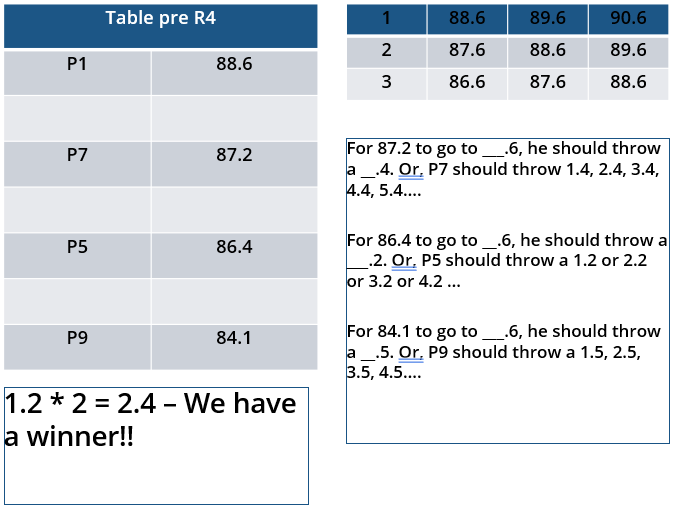
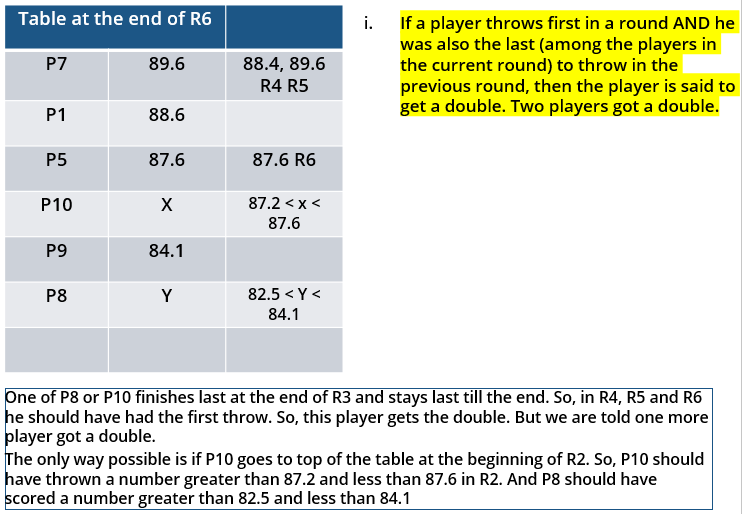
i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal.
ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.
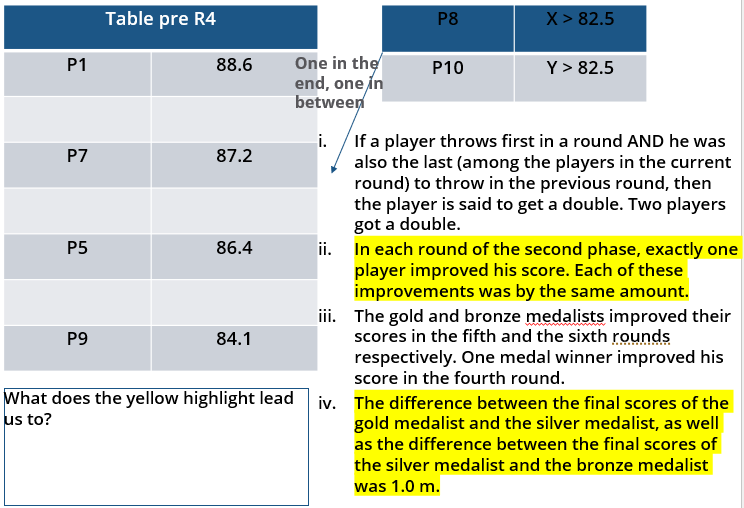
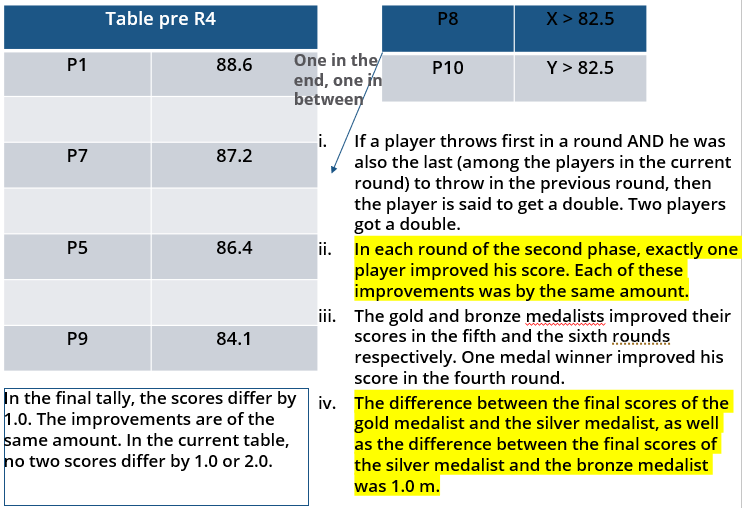
iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount.
iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round.
v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.
Which two players got the double?
Video Explanation
Explanatory Answer
Who threw the last javelin in the event?
Video Explanation
Explanatory Answer
What was the final score (in m) of the silver-medalist?
Video Explanation
Explanatory Answer
Which of the following can be the final score (in m) of P8?
Video Explanation
Explanatory Answer
By how much did the gold medalist improve his score (in m) in the second phase?
Video Explanation
Explanatory Answer
Which two players got the double?
Video Explanation
Explanatory Answer
Who threw the last javelin in the event?
Video Explanation
Explanatory Answer
The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal's approval ratio?
Video Explanation
Explanatory Answer
How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
Video Explanation
Explanatory Answer
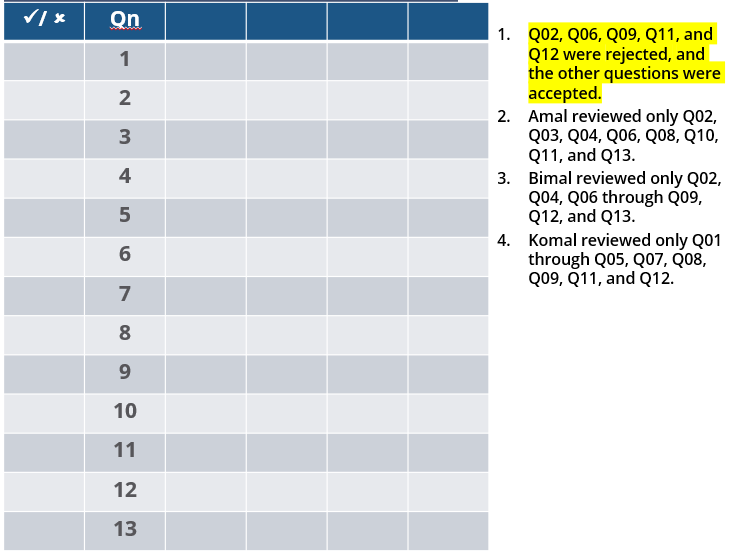
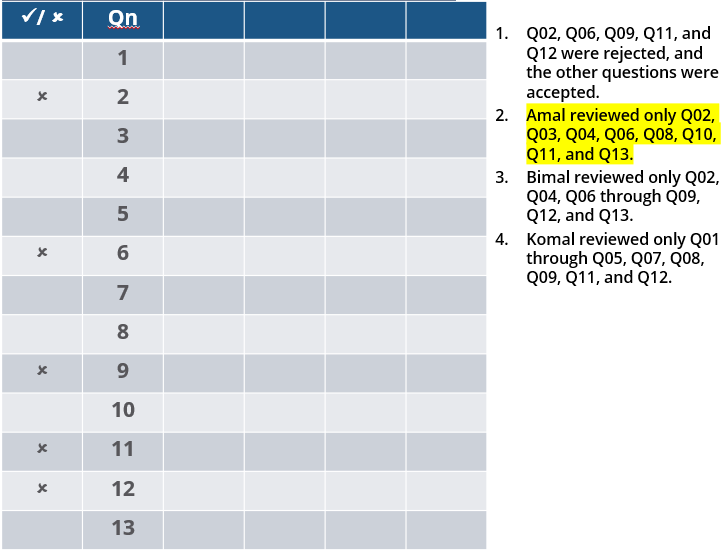
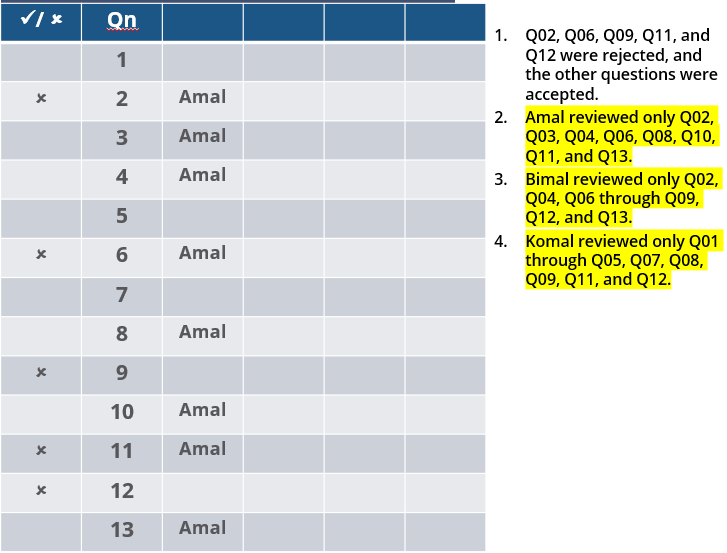
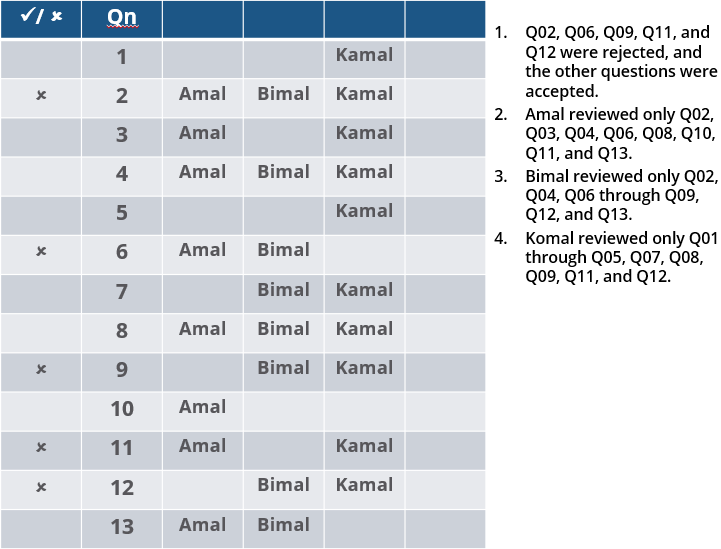
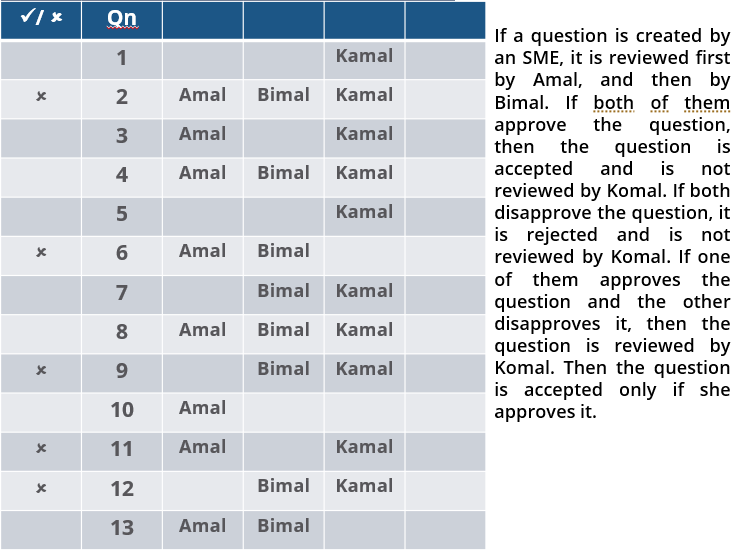
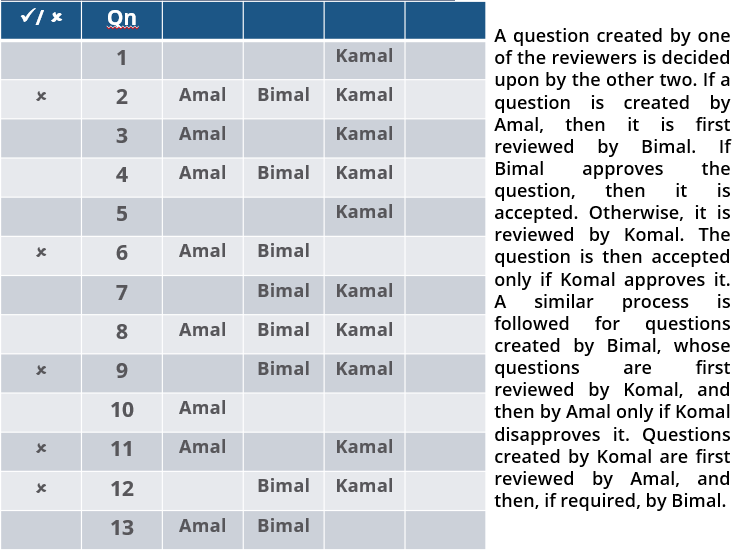
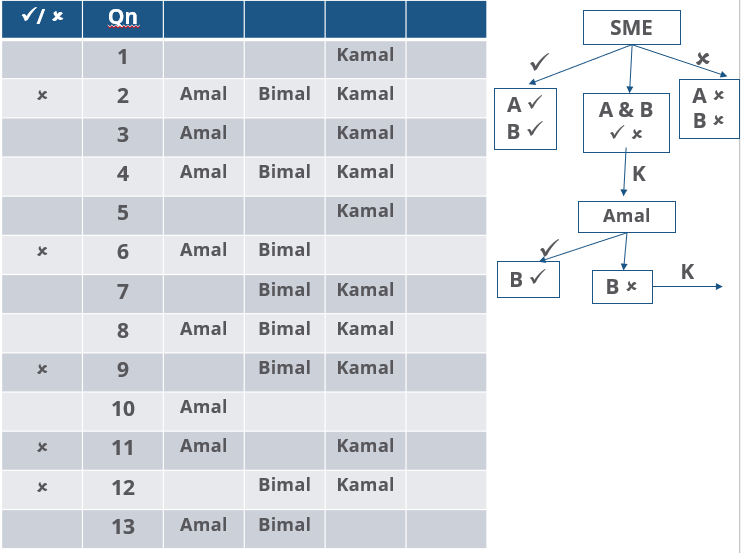
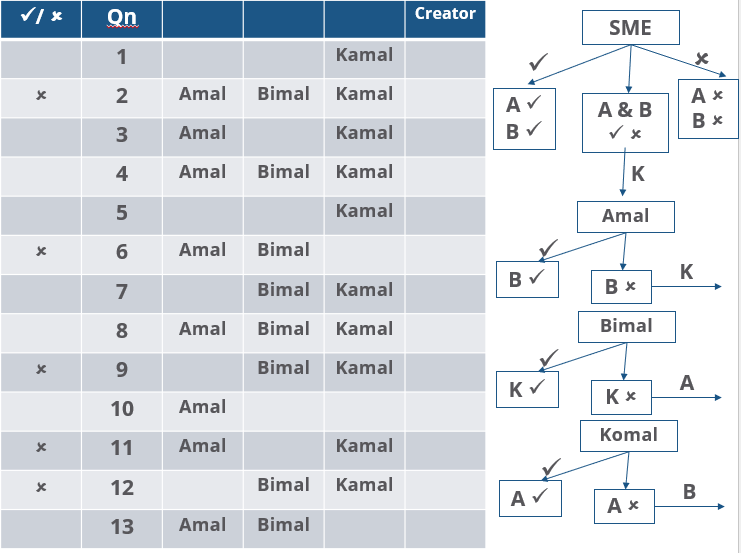
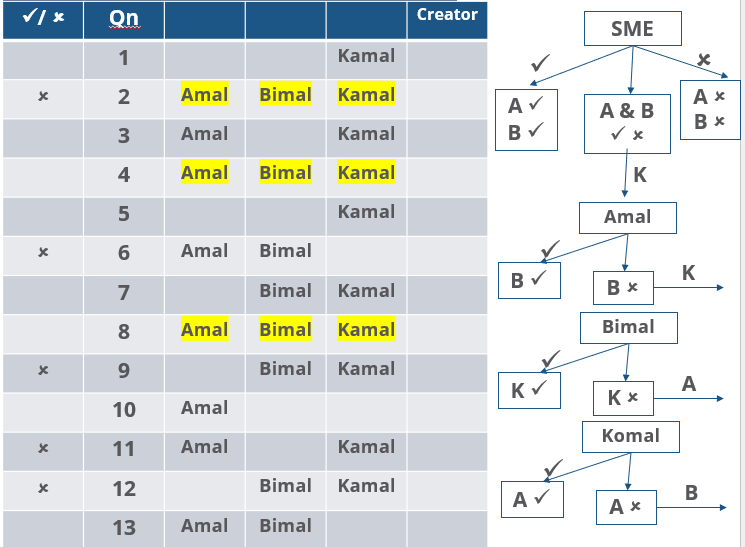
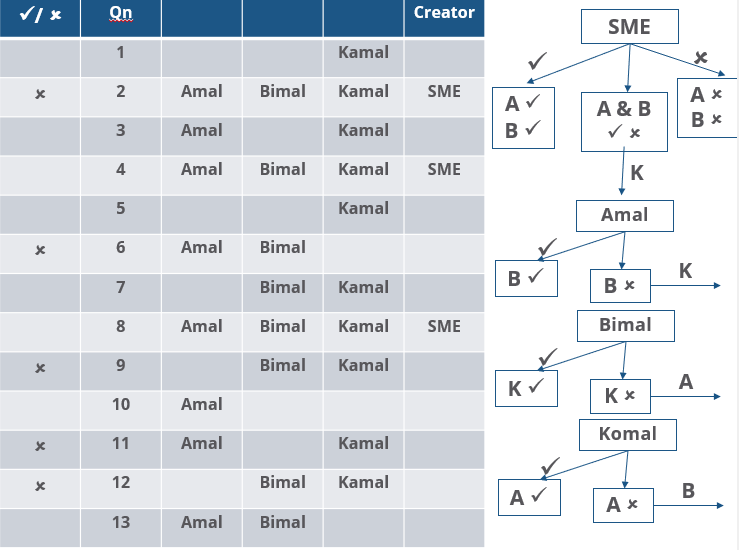
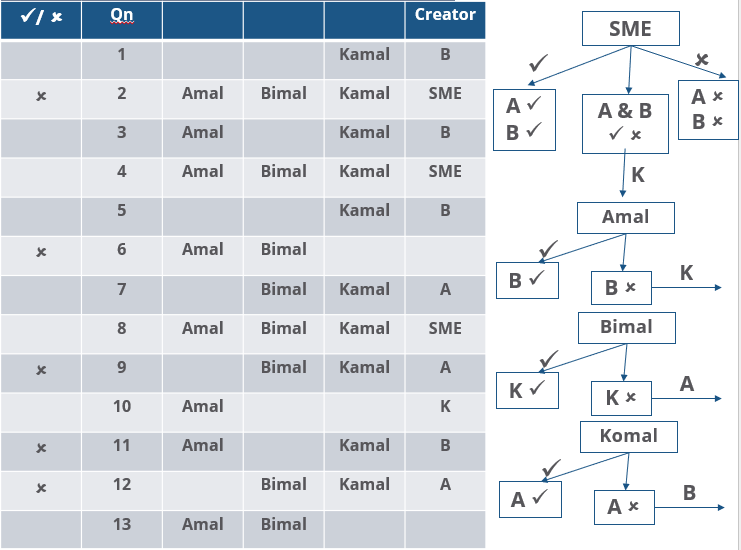
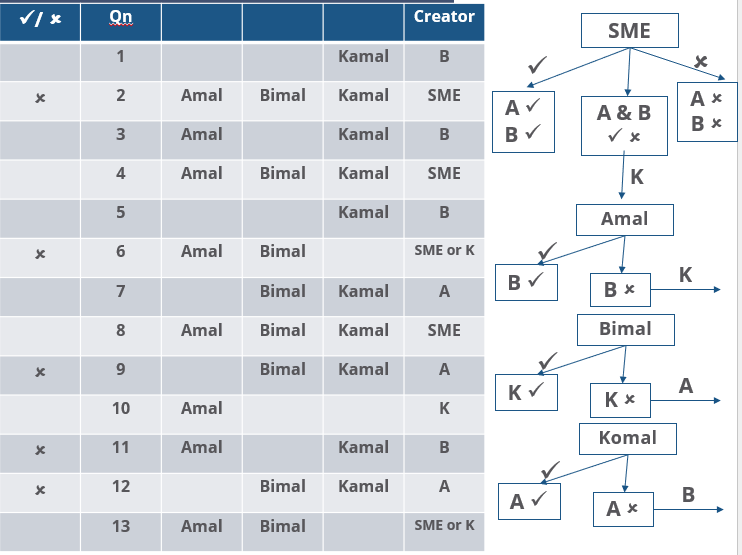
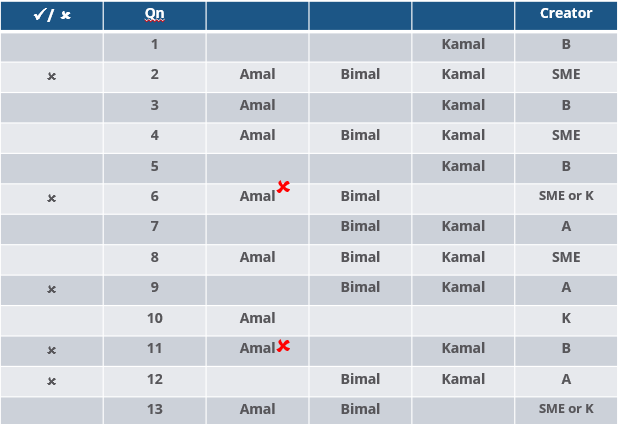
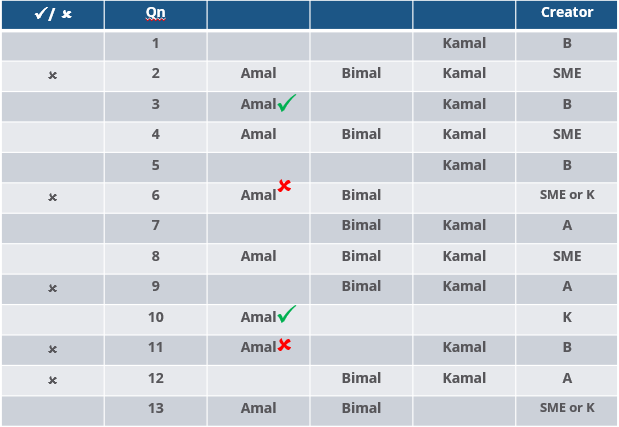
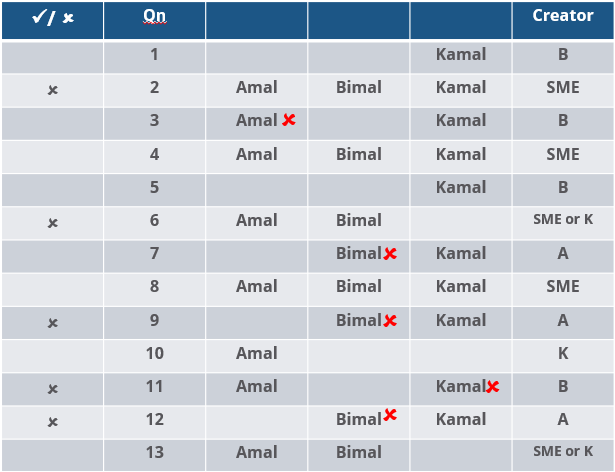
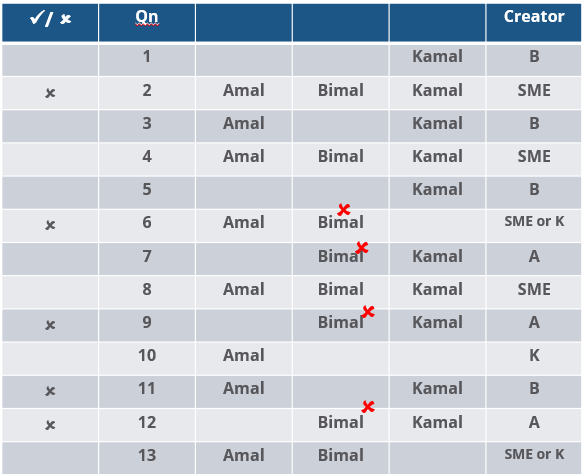
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external "subject matter experts" (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
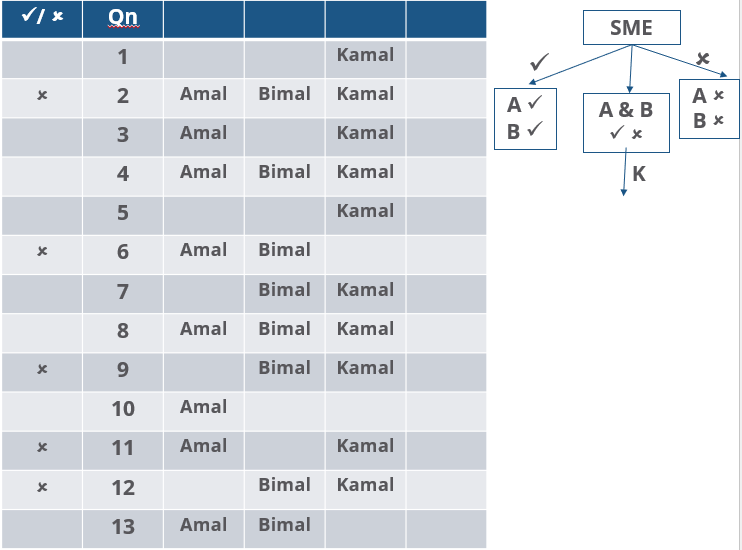
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
1. Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
2. Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
3. Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
4. Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
How many questions were DEFINITELY created by Komal?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY created by the SMEs?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY disapproved by Bimal?
Video Explanation
Explanatory Answer
The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal's approval ratio?
Video Explanation
Explanatory Answer
How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY created by Komal?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY created by the SMEs?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY disapproved by Bimal?
Video Explanation
Explanatory Answer
What BEST can be said about the distribution of object o1?
Video Explanation
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.
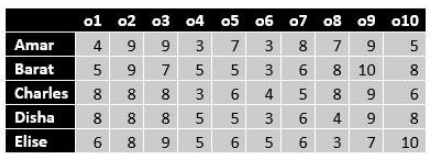
The value of any bundle by a person is the sum of that person's values of the objects in that bundle. A person X envies another person Y if X values Y's bundle more than X's own bundle.
For example, hypothetically suppose Amar's bundle consists of o1 and o2, and Barat's bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat's bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar's bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
1. If someone's value for an object is 10, then she/he received that object.
2. Objects o1, o2, and o3 were given to three different people.
3. Objects o1 and o8 were given to different people.
4. Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
5. Disha values her own bundle at an odd number. All others value their own bundles at an even number.
6. Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
What is Amar's value for his own bundle?
Video Explanation
What BEST can be said about the distribution of object o1?
Video Explanation
What is Amar's value for his own bundle?
Video Explanation
Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in north-south direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
Video Explanation
If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
Video Explanation
Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
Video Explanation
What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
Video Explanation
What is the minimum number of trains that are required to provide the service in this city?
Video Explanation
If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
Video Explanation
If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
Video Explanation
Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
Video Explanation
What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
Video Explanation
What is the minimum number of trains that are required to provide the service in this city?
Video Explanation
Which of the following could be the amount of funding that Tantra received?
(a) Rs. 66,000
(b) Rs. 165,000
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
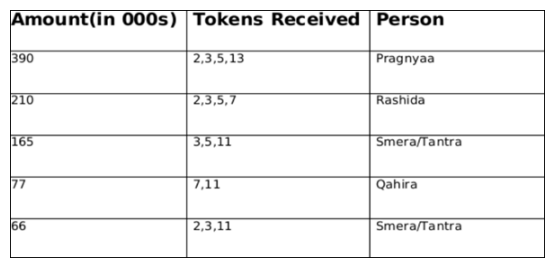
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000.
Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000.
The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
How many tokens did Qahira receive?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
Who among the following definitely received a token from Bithi but not from Dhanavi?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
How many tokens did Chhaya award?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
How many tokens did Smera receive?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
Which of the following could be the amount of funding that Tantra received?
(a) Rs. 66,000
(b) Rs. 165,000
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
How many tokens did Qahira receive?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
Who among the following definitely received a token from Bithi but not from Dhanavi?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
How many tokens did Chhaya award?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
How many tokens did Smera receive?
Video Explanation
Explanatory Answer
From, Statement 1 we know that Fatima gave token to 4 people ecept Qahira so the token number given by fatima is 3 and adhara gave token only to pragnyaa so the token number given by Adhara is 13
Therefore, we can also say that pragnyaa received 3,90,000 and qahira received 77,000 From statement 2, we know that Rahida received highest number of token and we already concluded that Pragnyaareceived a funding of 3,90,000 so we can say that Rashida received a funding of 2,10,000
Rashida did not received a token from Esther so we can also conclude that Esther so we can also conclude that Esther gave the token number
From Statement 3, we can conclude that Dhanavi gave a token of 7 and bethi gave a token of either 2 or 5 and similarly chhaya also gave a token of 2 or 5
Which of the following statement(s) is/are true?
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
Which of the following statement(s) is/are false?
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
If Harita scored goals in one more match as compared to Sarita, which of the following
statement(s) is/are necessarily true?
Statement-1: Amla scored goals in consecutive matches.
Statement-2: Sarita scored goals in consecutive matches.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
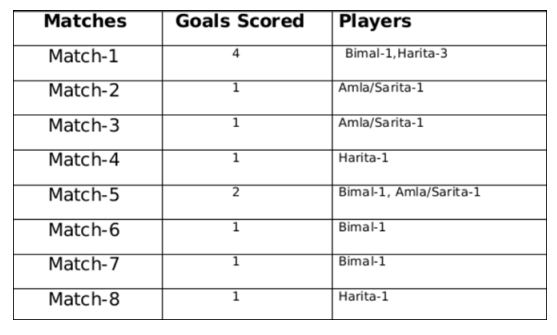
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals.
The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
How many goals were scored in Match 7?
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
Which of the following statement(s) is/are true?
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
Which of the following statement(s) is/are false?
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
If Harita scored goals in one more match as compared to Sarita, which of the following
statement(s) is/are necessarily true?
Statement-1: Amla scored goals in consecutive matches.
Statement-2: Sarita scored goals in consecutive matches.
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
How many goals were scored in Match 7?
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
Video Explanation
Explanatory Answer
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goal scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5)
From statement 4 we know that Bimal scored 4 goals and since harita scored more goals than bimal so we can say that harita scored 5 goals and the only case possible for total goals scored by each of the player is (1,2,4,5)
Now, using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which bimal scored will be 5 th ,6 th and 7 th matches as harita scored in 4 th and 8 the matches. From statement 5 and 6 we can conclude that the highest number of goals were scored in match 1 Let the no. Of goals scored in 3 rd and 7 th match be a each and no. Of goals scored in 1 st and 5 th match be b and c respectively.
Therefore, 2a+b+c=8
If a=1 then b+c=6 if a=2 then b+c= 4 therefore possible solution for b and c will be 1 and 3 and harita scored 5 goals in 3 matches therefore, we can see this is not possible because the no of goals scored in match1 becomes 4 Therefore, the only possibile solution is a=1 b=4 and c=2 And the remaing 3 goals were scored in the matcg 2,3 and 5 by amla and sarita in some order
How many female dancers are interested in attending a 2-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer.
Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event.
The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
How many boys are there in the class?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II.The number of female dancers who are interested in attending a 1-day event
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
What fraction of the class are interested in attending a 2-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
How many female dancers are interested in attending a 2-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
How many boys are there in the class?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II.The number of female dancers who are interested in attending a 1-day event
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
What fraction of the class are interested in attending a 2-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
Video Explanation
Explanatory Answer
No. Of girls= 15
Let the no. Of boys be Y
No. Of singers =6
No. Of boys who are singers = 4
Therefore, no. Of girls who are singers= 2
No. Of dancers =10
No. Of boys who are dancers = 4
No. Of Boys who are neither singers nor dancers = Y-10
No. Of girls who are neither singers nor dancers = 9
Let the number of girls who are interested in attending a 2-day event be a and the number of girls
who are dancers and are interested in 2-day event be B
Now, using statements 3 and 4, we get
2<0.18Y-4<6
6< 0.18Y <10
0.18Y should be integer for which Y should be a multiple of 50 and 0.18Y lies between 6 and 10;
therefore, the only possible value of Y is 50
From statement 5, we can say that,
4+0.4a-b= 5+b+1
Or, 0.4a= 2+2b
Or, a=5(1+b)
A should be a multiple of 5 and b is a whole number if a= 5 and then b= 1
On which day(s) did Pesmisto not have any new case?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that on Day 3, the number of cases will be zero for Pesmisto. Thus, the correct option is A.
Which of the two statements below is/are necessarily false?
Statement A: There were 2 new cases in Tyhrmisto on Day 3.
Statement B: There were no new cases in Pesmisto on Day 2.
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that both statements are false. Thus the correct option is D.
On how many days did Levmisto and Tyhrmisto have the same number of new cases?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
It can be concluded from the final table that the number of cases will be the same for all the days.
Thus, the correct option is D
Read the following information carefully, analyze it, and answer the question based on it.
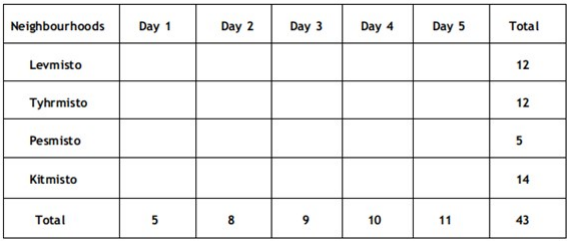
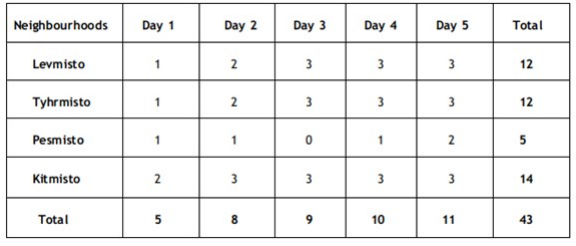
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
What BEST can be concluded about the total number of new cases in the city on Day 2?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the data, it can be concluded that the total number of cases on Day 2 is equal to 8. Thus, the correct option is D.
What BEST can be concluded about the number of new cases in Levmisto on Day 3?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that the total number of cases in Levmisto is 3 on day 3.
Thus, the correct option is C.
On which day(s) did Pesmisto not have any new case?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that on Day 3, the number of cases will be zero for Pesmisto. Thus, the correct option is A.
Which of the two statements below is/are necessarily false?
Statement A: There were 2 new cases in Tyhrmisto on Day 3.
Statement B: There were no new cases in Pesmisto on Day 2.
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that both statements are false. Thus the correct option is D.
On how many days did Levmisto and Tyhrmisto have the same number of new cases?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
It can be concluded from the final table that the number of cases will be the same for all the days.
Thus, the correct option is D
What BEST can be concluded about the total number of new cases in the city on Day 2?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the data, it can be concluded that the total number of cases on Day 2 is equal to 8. Thus, the correct option is D.
What BEST can be concluded about the number of new cases in Levmisto on Day 3?
Video Explanation
Explanatory Answer
From statement 6, it can be concluded that the total number of new cases is equal to 12+12+5+14 = 43.
Also, since the total number of cases in Kitmisto is 14, it can be concluded that the number of cases each day is either 2 or 3, where 3 cases are recorded on 4 days and 2 cases are recorded on 1 day.
From statement 4, it can be concluded that the number of new cases for Pesmisto will be 0,1,1,1, and 2, in any order(Since the total number of cases is 5, and the maximum number of new cases is 2).
In statement 3, it is given that the number of new cases kept increasing during the 5-day period.
Now, as it is already known that the maximum number of cases for Pesmisto is 2, the maximum total number of cases in a day(or on day 5) will be less than 12.
Let us consider the maximum number of cases on Day 5 as 10.
Thus the maximum number of cases possible for the remaining days will be 9, 8, 7, and 6. So, the total number of maximum cases possible for this case will be 40(less than 43).
Thus, the number of cases on Day 5 will be 11(i.e., b/w 10 and 11)
Now, if the number of cases on Day 4 is 9, the maximum number of cases possible for the remaining days will be 8, 7, and 6. Thus, the maximum number of cases, in this case, will be 41(less than 43).
So, the number of cases on day 4 will be 10.
Now, if the number of cases on Day 3 is 8, the number of cases on day 2 will be 7, and the maximum possible number of cases on Day 1 will be 6.
Thus, the number of cases, in this case, will be 42(less than 43).
Thus, the number of cases on day 3 will be 9, the number of cases on day 2 will be 8, and the number of cases on day 1 will be 5.
Since all the neighbourhood has at least one case on Day 1, the only possible combination will be 1, 1, 1, and 2 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, for the other 4 days, the number of cases in Kitmisto will be 3.
For day 5, the number of cases will be 3, 3, 2, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively(since the maximum number of cases in Pesmisto is 2).
And since Pesmisto only has the maximum number of cases on one day, the number of cases on day 4 will be 3, 3, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
On day 2, since Kitmisto is the only neighbourhood to have 3 cases, the number of cases on day 2 will be 2, 2, 1, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively.
Now, on day 3, the number of cases will be 3, 3, 0, and 3 for Levmisto, Tyhrmisto, Pesmisto and Kitmisto, respectively. Thus, the final table will be as follows:
From the final table, it can be concluded that the total number of cases in Levmisto is 3 on day 3.
Thus, the correct option is C.
Read the following information carefully, analyze it, and answer the question based on it.
In the following, a year corresponds to 1st of January of that year.
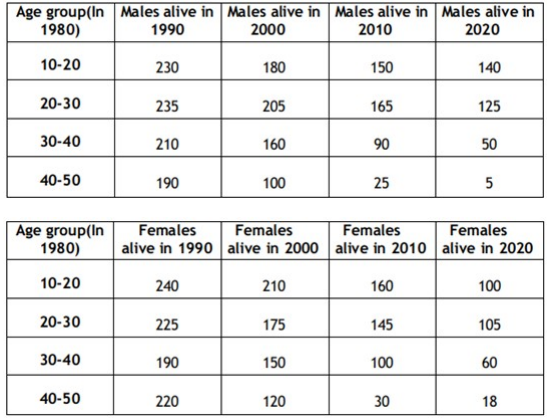
A study to determine the mortality rate for a disease began in 1980. The study chose 1000 males and 1000 females and followed them for forty years or until they died, whichever came first. The 1000 males chosen in 1980 consisted of 250 each of ages 10 to less than 20, 20 to less than 30, 30 to less than 40, and 40 to less than 50. The 1000 females chosen in 1980 also consisted of 250 each of ages 10 to less than 20, 20 to less than 30, 30 to less than 40, and 40 to less than 50.
The four figures below depict the age profile of those among the 2000 individuals who were still alive in 1990, 2000, 2010, and 2020. The blue bars in each figure represent the number of males in each age group at that point in time, while the pink bars represent the number of females in each age group at that point in time. The numbers next to the bars give the exact numbers being represented by the bars. For example, we know that 230 males among those tracked and who were alive in 1990 were aged between 20 and 30.
How many individuals who were being tracked and who were less than 30 years of age in 1980 survived until 2020?
Video Explanation
Explanatory Answer
The total number of male and female test cases in 1980 = 1000
The total number of males alive in 2000 = 180 + 205 + 160 + 100 = 645 Thus, the number of dead males in 2000 = 1000 - 645 = 355
Similarly, the total number of dead females in 2000 = 1000 - (210 + 175 + 150 + 120) = 1000 - 655 = 345
Thus, the required ratio = 355 : 345 = 71 : 69. Thus, the correct option is A.
How many of the males who were being tracked and who were between 20 and 30 years of age in 1980 died in the period 2000 to 2010?
Video Explanation
Explanatory Answer
The total number of male and female test cases in 1980 = 1000
The total number of males between 20 and 30 years of age in 1980 who died in 2000 = 205 The total number of males between 20 and 30 years of age in 1980 who died in 2010 = 165
Thus, the total number of males between 20 and 30 years of age in 1980 who died in the period 2000 to 2010 = 205 - 165 = 40
Hence, 40
How many of the females who were being tracked and who were between 20 and 30 years of age in 1980 died between the ages of 50 and 60?
Video Explanation
Explanatory Answer
The total number of male and female test cases in 1980 = 1000
We are given that there are 250 females from age 20-30 in 1980 and in 2000 these females age are from 40-50 but only 175 are alive in 2000.
In 2000 there were 175 females from age 40-50. If we assume that out of these, 30 females were of age 48 years in 2000 and they died in 2005, then there are 30 females who died at the age of 53.
If we assume that out of the 175 females, 30 females were of age 42 years in 2000, and they died in 2005, then 30 females died at the age of 47. Now, if we assume that there are 15 females of age 42 and 15 females of age 48 in the year 2000, and they all died in 2005, then we have 15 females who died at the age of 47 and 15 females who died at the age of 53.
So we can see that there are many cases possible. We are given that there were 250 females aged 20-30 in 1980, and in 2010, these females ages are from 50-60, but only 145 are alive in 2010.
In 2010 there were 145 females from age 50-60. If we assume that out of these, 40 females were of age 58 years in 2010 and they died in 2015, then there are 40 females who died at the age of 63.
If we assume that out of the 145 females, 40 females are of age 52 years age in 2010, and they died in 2015, then 40 females died at the age of 57. Now, if we assume that there are 15 females of age 52 and 25 females of age 58 in the year 2010, and they all died in 2015, then we have 15 females who died at the age of 57 and 25 females who died at the age of 63.
So we can see that again, there are many cases possible. In the first case, the range of values possible is from 0 to 30. In the second case, the range of values possible is from 0 to 40. So in total, we get a range of possible values from 0 to 70.
Thus, only one possible value of this question is not possible.
Hence, 30
