Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
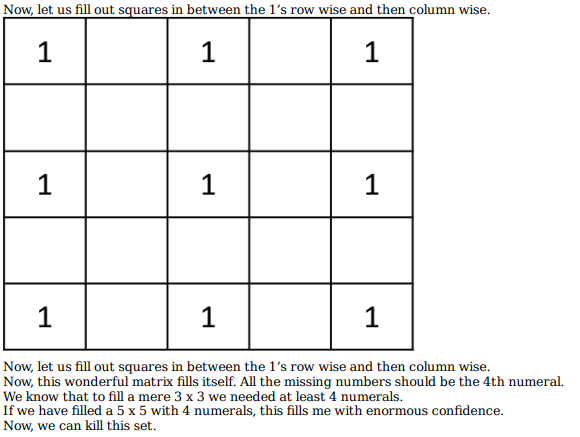
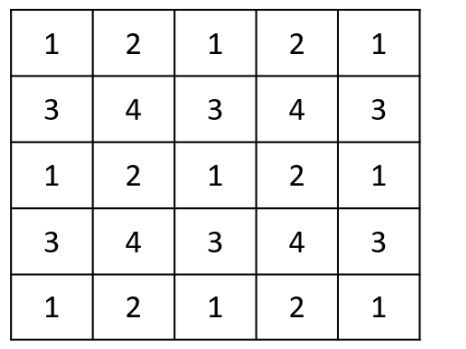
What is the minimum number of different numerals needed to fill a 5×5 square matrix? (TITA)
Video Explanation

What is the minimum possible number of satellites serving B exclusively?
Video Explanation

If at least 100 of the 1600 satellites were serving O, what can be said about the number of satellites serving S?
Video Explanation

If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?
Video Explanation

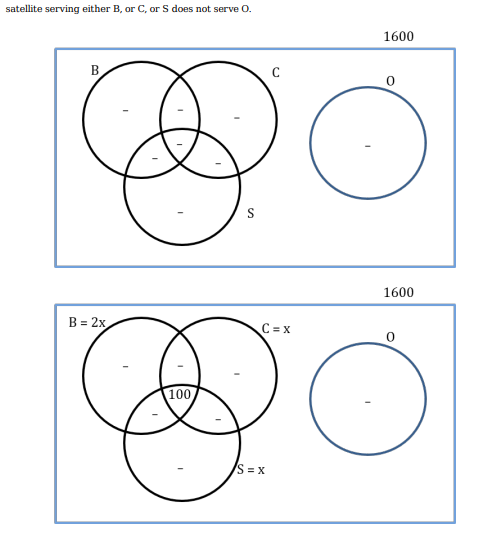
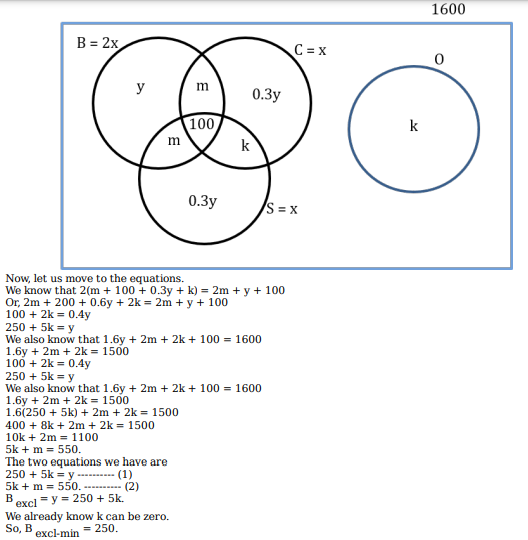
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
What best can be said about the number of satellites serving C?
Video Explanation

What is the minimum possible number of satellites serving B exclusively?
Video Explanation

If at least 100 of the 1600 satellites were serving O, what can be said about the number of satellites serving S?
Video Explanation

If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?
Video Explanation

What best can be said about the number of satellites serving C?
Video Explanation



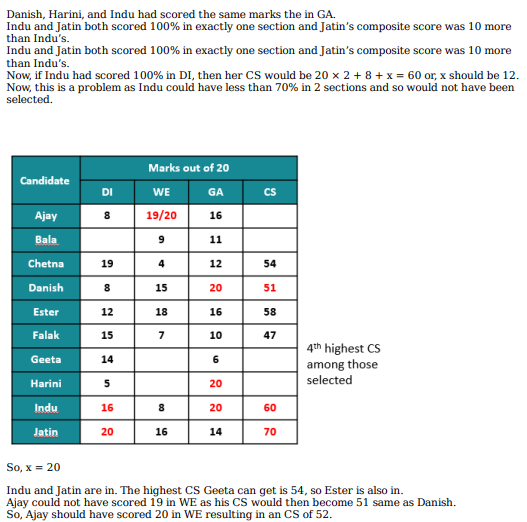
Which of the following statements MUST be true?
1.Jatin's composite score was more than that of Danish.
2. Indu scored less than Chetna in DI.
3. Jatin scored more than Indu in GA.
Video Explanation

Which of the following statements MUST be true?
1.Jatin's composite score was more than that of Danish.
2. Indu scored less than Chetna in DI.
3. Jatin scored more than Indu in GA.
Video Explanation

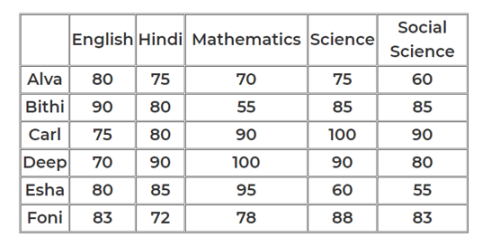
What BEST can be concluded about the students who missed the Science examination?
Video Explanation

How many out of these six students missed exactly one examination?
Video Explanation

For how many students can we be definite about which examinations they missed?
Video Explanation

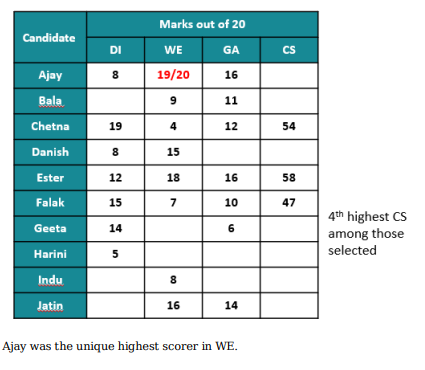
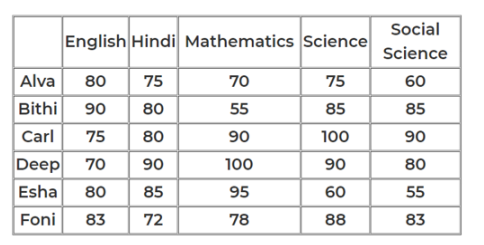
In a certain board examination, students were to appear for examination in five subjects: English, Hindi, Mathematics, Science and Social Science. Due to a certain emergency situation, a few of the examinations could not be conducted for some students. Hence, some students missed one examination and some others missed two examinations. Nobody missed more than two examinations.
The board adopted the following policy for awarding marks to students. If a student appeared in all five examinations, then the marks awarded in each of the examinations were on the basis of the scores obtained by them in those examinations.
If a student missed only one examination, then the marks awarded in that examination was the average of the best three among the four scores in the examinations they appeared for.
If a student missed two examinations, then the marks awarded in each of these examinations was the average of the best two among the three scores in the examinations they appeared for.
The marks obtained by six students in the examination are given in the table below. Each of them missed either one or two examinations.

The following facts are also known.
I. Four of these students appeared in each of the English, Hindi, Science, and Social Science examinations.
II. The student who missed the Mathematics examination did not miss any other examination.
Ill. One of the students who missed the Hindi examination did not miss any other examination. The other student who missed the Hindi examination also missed the Science examination.
Who among the following did not appear for the Mathematics examination?
Video Explanation

Which students did not appear for the English examination?
Video Explanation

What BEST can be concluded about the students who did not appear for the Hindi examination?
Video Explanation

What BEST can be concluded about the students who missed the Science examination?
Video Explanation

How many out of these six students missed exactly one examination?
Video Explanation

For how many students can we be definite about which examinations they missed?
Video Explanation

Who among the following did not appear for the Mathematics examination?
Video Explanation

Which students did not appear for the English examination?
Video Explanation

What BEST can be concluded about the students who did not appear for the Hindi examination?
Video Explanation

Which institutes and vendors had more than one contracts in any year?
Video Explanation

In how many years during this period was there only one contract?
Video Explanation

What BEST can be concluded about the number of contracts in 2010?
Video Explanation

Which institutes had multiple contracts during the same year?
Video Explanation

Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
In which of the following years were there two or more contracts?
Video Explanation

In how many years during this period was there only one contract?
Video Explanation

What BEST can be concluded about the number of contracts in 2010?
Video Explanation

Which institutes had multiple contracts during the same year?
Video Explanation

Which institutes and vendors had more than one contracts in any year?
Video Explanation

In which of the following years were there two or more contracts?
Video Explanation

Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation

Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation

If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation

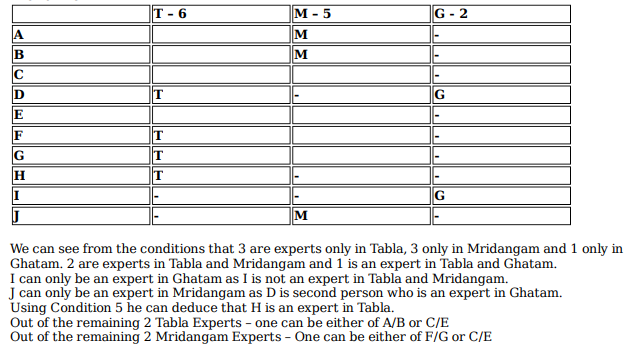
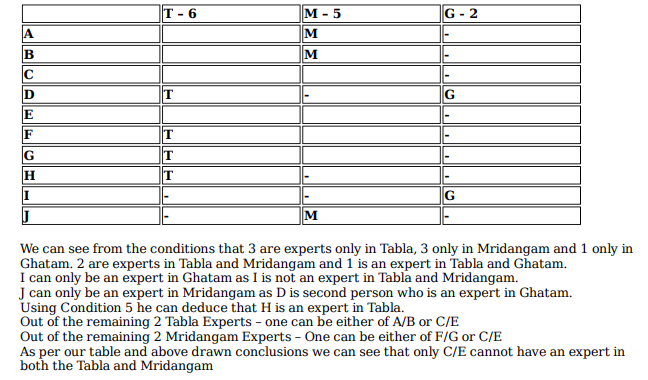
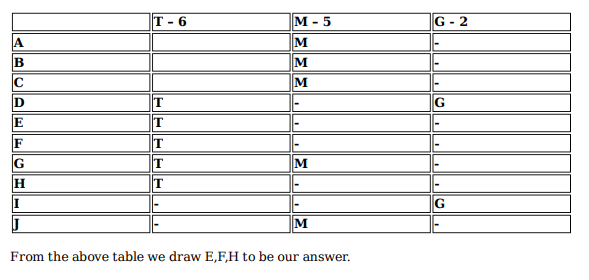
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation

Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation

Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation

If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation

Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation

Which of the following statements is necessarily true?
Video Explanation

If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation

If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation

If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation

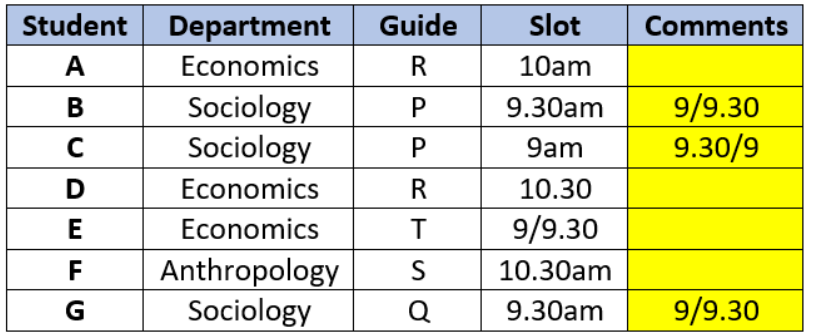
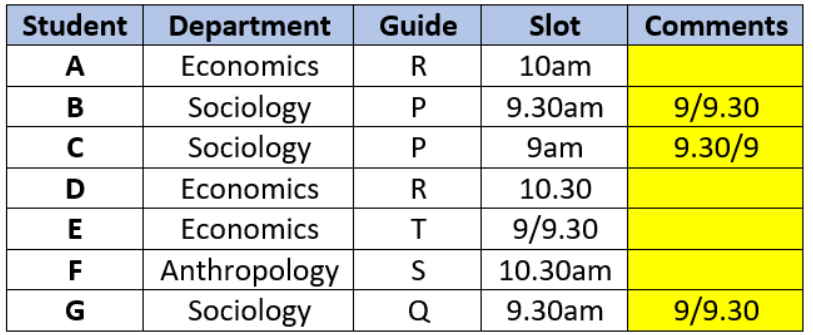
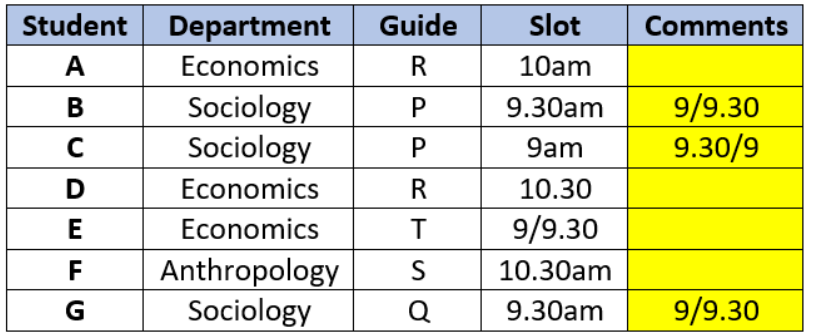
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Which of the following statements is necessarily true?
Video Explanation

If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation

If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation

If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation

The number of patients who were treated with medicine type D was:
Video Explanation

1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
a. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine type B?
Video Explanation

The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation

How many patients were treated with medicine types B and D only?
Video Explanation

The number of patients who were treated with medicine type D was:
Video Explanation

How many patients were treated with medicine type B?
Video Explanation

The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation

How many patients were treated with medicine types B and D only?
Video Explanation

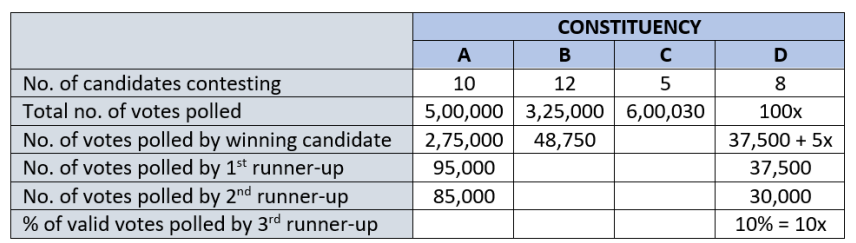
In an election several candidates contested for a constituency. In any constituency, the winning candidate was the one who polled the highest number of votes, the first runner up was the one who polled the second highest number of votes, the second runner up was the one who polled the third highest number of votes, and so on. There were no ties (in terms of number of votes polled by the candidates) in any of the constituencies in this election.
In an electoral system, a security deposit is the sum of money that a candidate is required to pay to the election commission before he or she is permitted to contest. Only the defeated candidates (i.e., one who is not the winning candidate) who fail to secure more than one sixth of the valid votes polled in the constituency, lose their security deposits.
The following table provides some incomplete information about votes polled in four constituencies: A, B, C and D, in this election.

The following additional facts are known:
1. The first runner up polled 10,000 more votes than the second runner up in constituency A. 2. None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000.
3. The winning candidate in constituency D polled 5% of valid votes more than that of the first runner up. All the candidates who lost their security deposits while contesting for this constituency, put together, polled 35% of the valid votes.
How many candidates who contested in constituency B lost their security deposit?
Video Explanation

What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation

What was the number of valid votes polled in constituency D?
Video Explanation

How many candidates who contested in constituency B lost their security deposit?
Video Explanation

What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation

What was the number of valid votes polled in constituency D?
Video Explanation

What was the increase in sales amount, in Crore Rupees, in the Apparel department of Mumbai from 2018 to 2019?
Video Explanation

Previous year papers
2024
2023
2022
2021
2020
2019
2018