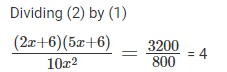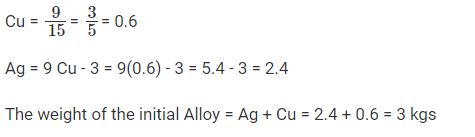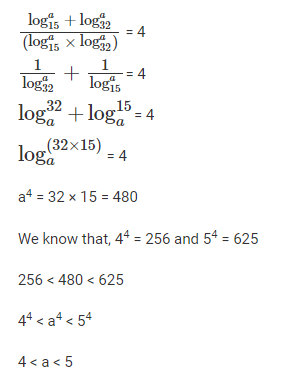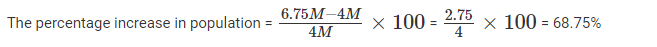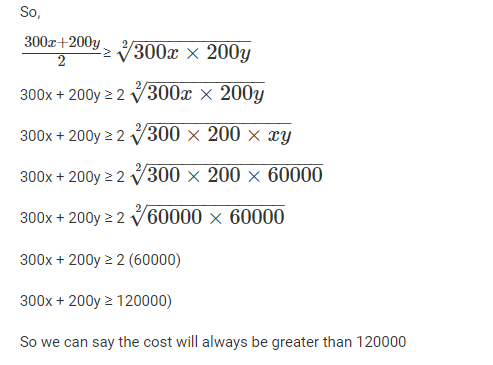Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
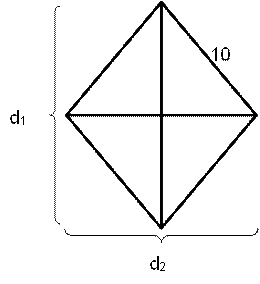
The number of distinct pairs of integers (m,n) satisfying |1+mn| < |m + n| < 5 is
Video Explanation

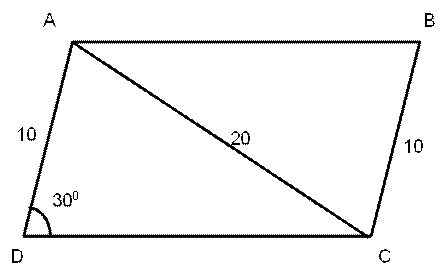
Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle ∠ADC is equal to 30° then the area of the parallelogram, in sq. cm, is
Video Explanation

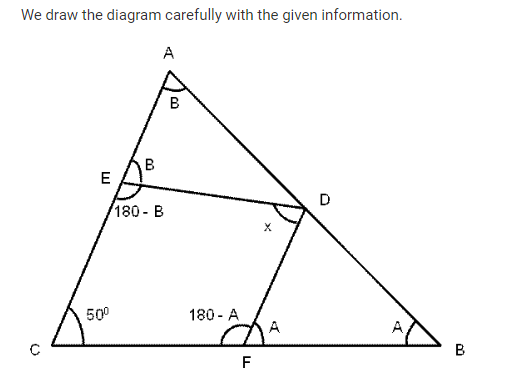
In a triangle ABC, ∠ BCA = 50°. D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF, then ∠FDE, in degrees, is equal to
Video Explanation

A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
Video Explanation

One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is
Video Explanation

If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
Video Explanation

The arithmetic mean of scores of 25 students in an examination is 50. Five of these students top the examination with the same score. If the scores of the other students are distinct integers with the lowest being 30, then the maximum possible score of the toppers is
Video Explanation

A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is
Video Explanation

One part of a hostel's monthly expenses is fixed, and the other part is proportional to the number of its boarders. The hostel collects ₹ 1600 per month from each boarder. When the number of boarders is 50, the profit of the hostel is ₹ 200 per boarder, and when the number of boarders is 75, the profit of the hostel is ₹ 250 per boarder. When the number of boarders is 80, the total profit of the hostel, in INR, will be
Video Explanation

If 3x + 2|y| + y = 7 and x + |x| + 3y = 1, then x + 2y is
Video Explanation

In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
Video Explanation

Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is
Video Explanation

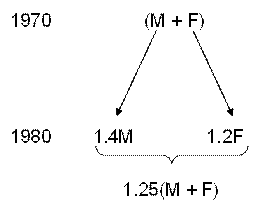
The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
Video Explanation


Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in north-south direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
Video Explanation

If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
Video Explanation

Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
Video Explanation

What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
Video Explanation

What is the minimum number of trains that are required to provide the service in this city?
Video Explanation

If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
Video Explanation

If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
Video Explanation

Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
Video Explanation

What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
Video Explanation

What is the minimum number of trains that are required to provide the service in this city?
Video Explanation

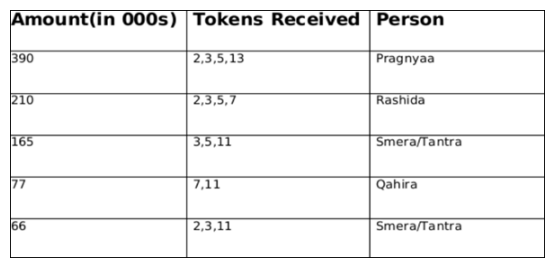
Which of the following could be the amount of funding that Tantra received?
(a) Rs. 66,000
(b) Rs. 165,000
Video Explanation

Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000.
Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000.
The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
How many tokens did Qahira receive?
Video Explanation

Who among the following definitely received a token from Bithi but not from Dhanavi?
Video Explanation

How many tokens did Chhaya award?
Video Explanation

How many tokens did Smera receive?
Video Explanation

Which of the following could be the amount of funding that Tantra received?
(a) Rs. 66,000
(b) Rs. 165,000
Video Explanation

How many tokens did Qahira receive?
Video Explanation

Who among the following definitely received a token from Bithi but not from Dhanavi?
Video Explanation

How many tokens did Chhaya award?
Video Explanation

How many tokens did Smera receive?
Video Explanation

Which of the following statement(s) is/are true?
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.
Video Explanation

Which of the following statement(s) is/are false?
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.
Video Explanation

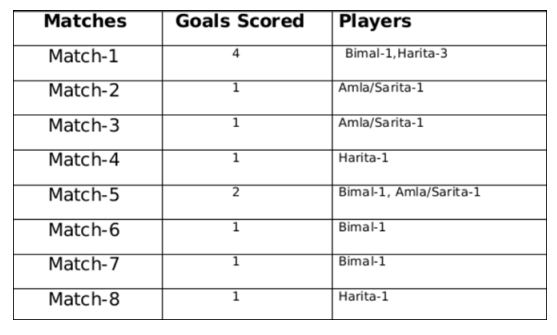
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals.
The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
Video Explanation

Which of the following statement(s) is/are true?
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.
Video Explanation

Which of the following statement(s) is/are false?
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.
Video Explanation

Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
Video Explanation

How many female dancers are interested in attending a 2-day event?
Video Explanation

There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer.
Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event.
The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
How many boys are there in the class?
Video Explanation

Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II.The number of female dancers who are interested in attending a 1-day event
Video Explanation

What fraction of the class are interested in attending a 2-day event?
Video Explanation

What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
Video Explanation

How many female dancers are interested in attending a 2-day event?
Video Explanation

How many boys are there in the class?
Video Explanation

Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II.The number of female dancers who are interested in attending a 1-day event
Video Explanation

What fraction of the class are interested in attending a 2-day event?
Video Explanation

What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
Video Explanation

The average weight of students in a class increases by 600 gm when some new students join the class. If the average weight of the new students is 3 kg more than the average weight of the original students, then the ratio of the number of original students to the number of new students is
Video Explanation

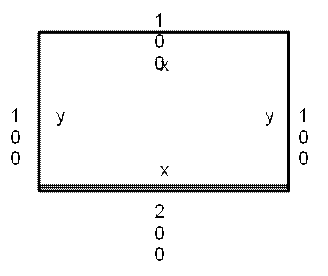
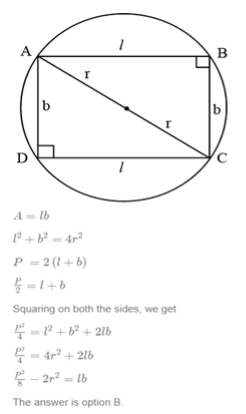
All the vertices of a rectangle lie on a circle of radius R. If the perimeter of the rectangle is P, then the area of the rectangle is
Video Explanation

Previous year papers
2023
2022
2021
2020
2019
2018