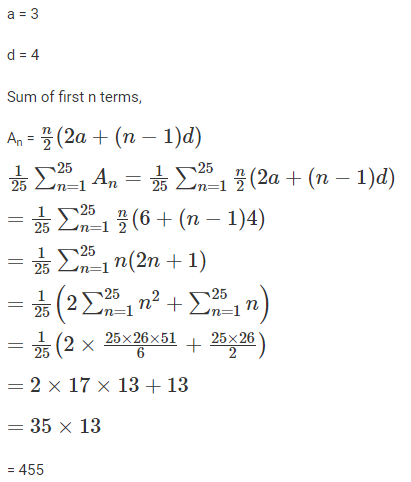Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
13.2K
Learners
asked the doubt

Previous Year Questions
A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is
Video Explanation

The average of all 3-digit terms in the arithmetic progression 38, 55, 72, ., is
Video Explanation

A group of N people worked on a project. They finished 35% of the project by working 7 hours a day for 10 days. Thereafter, 10 people left the group and the remaining people finished the rest of the project in 14 days by working 10 hours a day. Then the value of N is
Video Explanation

Moody takes 30 seconds to finish riding an escalator if he walks on it at his normal speed in the same direction. He takes 20 seconds to finish riding the escalator if he walks at twice his normal speed in the same direction. If Moody decides to stand still on the escalator, then the time, in seconds, needed to finish riding the escalator is
Video Explanation

Two cars travel from different locations at constant speeds. To meet each other after starting at the same time, they take 1.5 hours if they travel towards each other, but 10.5 hours if they travel in the same direction. If the speed of the slower car is 60 km/hr, then the distance traveled, in km, by the slower car when it meets the other car while traveling towards each other, is
Video Explanation

Nitu has an initial capital of ₹20,000. Out of this, she invests ₹8,000 at 5.5% in bank A, ₹5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in bank C alone, then her annual interest income, in rupees, would have been
Video Explanation

The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is
Video Explanation

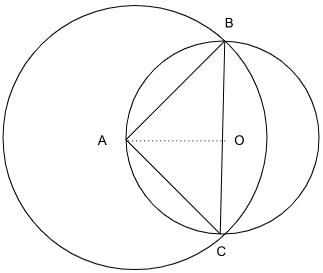
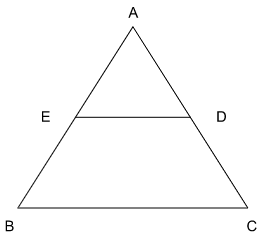
Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is
Video Explanation

In an examination, the average marks of students in sections A and B are 32 and 60, respectively. The number of students in section A is 10 less than that in section B. If the average marks of all the students across both the sections combined is an integer, then the difference between the maximum and minimum possible number of students in section A is
Video Explanation

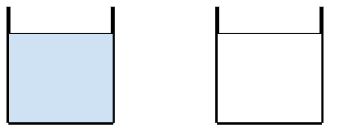
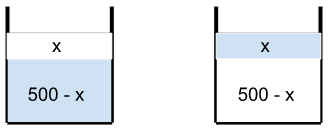
A glass contains 500 cc of milk and a cup contains 500 cc of water. From the glass, 150 cc of milk is transferred to the cup and mixed thoroughly. Next, 150 cc of this mixture is transferred from the cup to the glass. Now, the amount of water in the glass and the amount of milk in the cup are in the ratio
Video Explanation

What best can be concluded about the total amount of money raised in 2015?
Video Explanation

What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
Video Explanation

If Elavalaki raised Rs. 3 crores in 2013, then what is the smallest possible total amount of money (in Rs. crores) that could have been raised by all the companies in 2012?
Video Explanation

If the total amount of money raised in 2014 is Rs. 12 crores, then which of the following is not possible?
Video Explanation

Read the following information carefully, analyze it, and answer the question based on it.
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
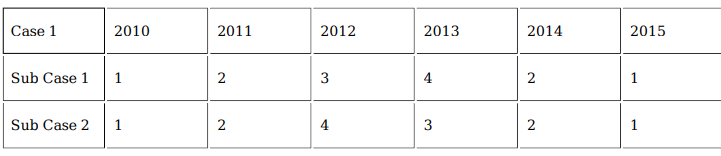
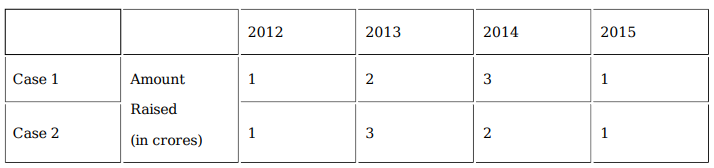
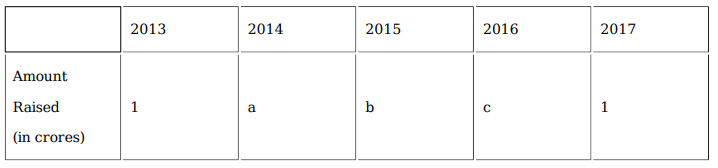
The table below provides partial information about the five firms.
For which firm(s) can the amounts raised by them be concluded with certainty in each year?
Video Explanation

What best can be concluded about the total amount of money raised in 2015?
Video Explanation

What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
Video Explanation

If Elavalaki raised Rs. 3 crores in 2013, then what is the smallest possible total amount of money (in Rs. crores) that could have been raised by all the companies in 2012?
Video Explanation

If the total amount of money raised in 2014 is Rs. 12 crores, then which of the following is not possible?
Video Explanation

For which firm(s) can the amounts raised by them be concluded with certainty in each year?
Video Explanation

Read the following information carefully, analyze it, and answer the question based on it.
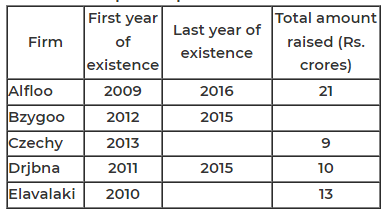
Three participants – Akhil, Bimal and Chatur participate in a random draw competition for five days. Every day, each participant randomly picks up a ball numbered between 1 and 9. The number on the ball determines his score on that day. The total score of a participant is the sum of his scores attained in the five days. The total score of a day is the sum of participants' scores on that day. The 2-day average on a day, except on Day 1, is the average of the total scores of that day and of the previous day. For example, if the total scores of Day 1 and Day 2 are 25 and 20, then the 2-day average on Day 2 is calculated as 22.5. Table 1 gives the 2-day averages for Days 2 through 5.

Participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. If there is a tie, all participants with the tied score are awarded the best available rank. For example, if on a day Akhil, Bimal, and Chatur score 8, 7 and 7 respectively, then their ranks will be 1, 2 and 2 respectively on that day. These ranks are given in Table 2.
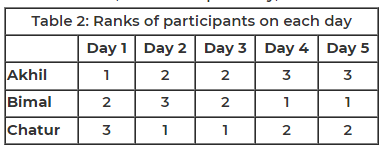
The following information is also known.
1. Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil's score on Day 4.
2. The total score on Day 3 is the same as the total score on Day 4.
3. Bimal's scores are the same on Day 1 and Day 3.
What is the minimum possible total score of Bimal?
Video Explanation

If the total score of Bimal is a multiple of 3, what is the score of Akhil on Day 2?
Video Explanation

If Akhil attains a total score of 24, then what is the total score of Bimal?
Video Explanation

What is the minimum possible total score of Bimal?
Video Explanation

If the total score of Bimal is a multiple of 3, what is the score of Akhil on Day 2?
Video Explanation

If Akhil attains a total score of 24, then what is the total score of Bimal?
Video Explanation

Read the following information carefully, analyze it, and answer the question based on it.
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
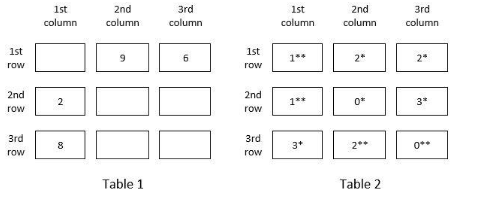
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
What is the total number of coins in all the boxes in the 3rd row?
Video Explanation

How many boxes have at least one sack containing 9 coins?
Video Explanation

How many sacks have exactly one coin?
Video Explanation

In how many boxes do all three sacks contain different numbers of coins?
Video Explanation

What is the total number of coins in all the boxes in the 3rd row?
Video Explanation

How many boxes have at least one sack containing 9 coins?
Video Explanation

How many sacks have exactly one coin?
Video Explanation

In how many boxes do all three sacks contain different numbers of coins?
Video Explanation

The area of the quadrilateral bounded by the Y-axis, the line X =5, and the lines |x−y|−|x−5|=2, is
Video Explanation

In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP : PQ : QC is
Video Explanation

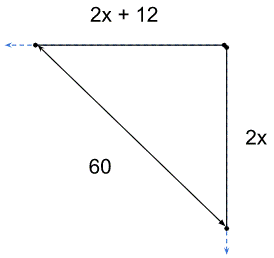
Two ships meet mid-ocean, and then, one ship goes south and the other ship goes west, both travelling at constant speeds. Two hours later, they are 60 km apart. If the speed of one of the ships is 6 km per hour more than the other one, then the speed, in km per hour, of the slower ship is
Video Explanation

Previous year papers
2023
2022
2021
2020
2019
2018